题目内容
(本小题满分12分)
已知椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() 是椭圆上两个不同的动点.
是椭圆上两个不同的动点.
(I)求直线![]() 与
与![]() 交点的轨迹C的方程;
交点的轨迹C的方程;
(II)若过点F(0,2)的动直线l与曲线C交于A ,B两点,![]() ,问在y轴上是否存在定点E,使得
,问在y轴上是否存在定点E,使得![]() ?若存在,求出E点的坐标;若不存在,说明理由.
?若存在,求出E点的坐标;若不存在,说明理由.
(本小题满分12分)
解:(Ⅰ)方法一:设直线![]() 与
与![]() 的交点为
的交点为![]() ,
,
∵![]() 是椭圆
是椭圆![]() 的上、下顶点,
的上、下顶点,
∴![]() …………………1分
…………………1分
![]() ,
,![]() ,
,
两式相乘得![]() .………………………3分
.………………………3分
而![]() 在椭圆
在椭圆![]() (
(![]() )上,
)上,
所以![]() ,即
,即![]() ,所以
,所以![]() .……………4分
.……………4分
又当![]() 时,不合题意,去掉顶点.
时,不合题意,去掉顶点.
∴直线![]() 与
与![]() 的交点的轨迹
的交点的轨迹![]() 的方程是
的方程是![]() ;……………5分
;……………5分
方法二:设直线![]() 与
与![]() 的交点为
的交点为![]() ,
,
∵![]() 是椭圆
是椭圆![]() 的上、下顶点,
的上、下顶点,
∴![]() …………………1分
…………………1分
∵![]() 共线,
共线,![]() 共线,
共线,
∴![]() …………①
…………①
![]() …………②…………………3分
…………②…………………3分
①![]() ②得
②得 ,
,
又∵![]() 即
即![]() ,
,
∴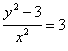 ,即
,即![]() ,
,
∴直线![]() 与
与![]() 的交点的轨迹
的交点的轨迹![]() 的方程是
的方程是![]() ;(
;(![]() )……………5分
)……………5分
(Ⅱ)假设存在满足条件的直线,由已知,其斜率一定存在,设其斜率为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
由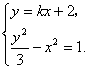 得
得![]() ,
,
![]() .…………………6分
.…………………6分
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]()
![]() ,
,![]() ,
,
![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
即![]() .………………………8分
.………………………8分
将![]() ,
,![]() ,
,![]() 代入上式并整理得
代入上式并整理得![]() ,…………………9分
,…………………9分
当![]() 时,
时,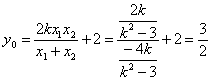 ,
,
当![]() 时,
时,![]() ,
,![]() 恒成立,
恒成立,
…………………11分
所以,
在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() ,点
,点![]() 的坐标为
的坐标为![]() .………12分
.………12分 www..com
www..com

练习册系列答案
相关题目