题目内容
(本小题满分12分)
如图,三棱柱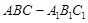 中,
中,
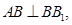
 ,
, 为
为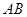 的中点,且
的中点,且 .
.
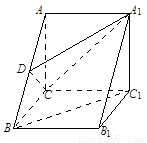
(1)求证: ∥平面
∥平面 ;
;
(2)求 与平面
与平面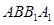 所成角的大小.
所成角的大小.
【答案】
(1)证明线面平行,只要通过线面平行的判定定理来证明即可。
(2)∠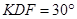 .
.
【解析】
试题分析:⑴证明:如图一,连结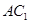 与
与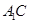 交于点
交于点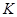 ,连结
,连结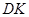 .
.
在△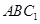 中,
中,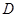 、
、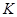 为中点,∴
为中点,∴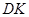 ∥
∥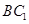 .
(4分)
.
(4分)
又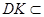 平面
平面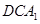 ,
,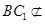 平面
平面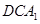 ,∴
,∴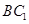 ∥平面
∥平面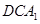 . (6分)
. (6分)

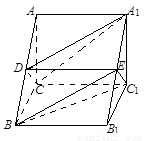
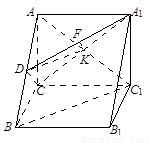
图一 图二 图三
⑵证明:(方法一)如图二,∵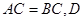 为
为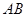 的中点,∴
的中点,∴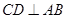 .
.
又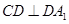 ,
,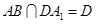 ,∴
,∴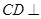 平面
平面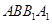 .
(8分)
.
(8分)
取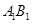 的中点
的中点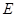 ,又
,又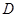 为
为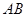 的中点,∴
的中点,∴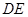 、
、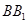 、
、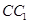 平行且相等,
平行且相等,
∴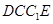 是平行四边形,∴
是平行四边形,∴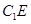 、
、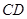 平行且相等.
平行且相等.
又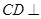 平面
平面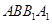 ,∴
,∴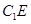
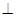 平面
平面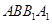 ,∴∠
,∴∠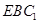 即所求角. (10分)
即所求角. (10分)
由前面证明知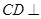 平面
平面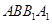 ,∴
,∴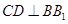 ,
,
又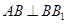 ,
,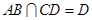 ,∴
,∴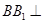 平面
平面 ,∴此三棱柱为直棱柱.
,∴此三棱柱为直棱柱.
设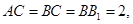 ∴
∴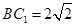 ,
,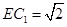 ,∠
,∠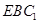 =
=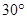 .
(12分)
.
(12分)
(方法二)如图三,∵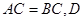 为
为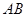 的中点,∴
的中点,∴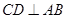 .
.
又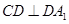 ,
,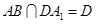 ,∴
,∴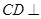 平面
平面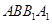 .
(8分)
.
(8分)
取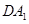 的中点
的中点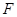 ,则
,则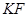 ∥
∥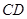 ,∴
,∴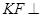 平面
平面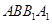 .
.
∴∠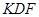 即
即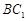 与平面
与平面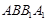 所成的角.
(10分)
所成的角.
(10分)
由前面证明知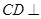 平面
平面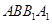 ,∴
,∴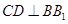 ,
,
又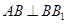 ,
,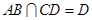 ,∴
,∴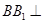 平面
平面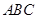 ,∴此三棱柱为直棱柱.
,∴此三棱柱为直棱柱.
设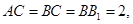 ∴
∴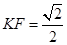 ,
,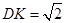 ,∴∠
,∴∠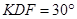 . (12分)
. (12分)
考点:线面平行,线面角
点评:主要是考查了线面角的求解,以及线面平行的判定定理的运用,属于基础题。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目