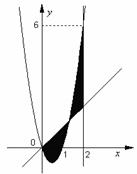
题目内容
如图,已知二次函数![]() ,直线
,直线![]() ,直线
,直线![]()
![]() (其中
(其中![]() ,
,![]() 为常数);.若直线
为常数);.若直线![]() 的图象以及
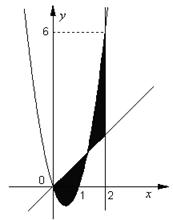
的图象以及![]() 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(Ⅰ)求![]() ;
;
(Ⅱ)求阴影面积s关于t的函数![]() 的解析式;
的解析式;
(Ⅲ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数m的取值范围.
的三条切线,求实数m的取值范围.
(1)![]() (2)
(2)![]()
![]() ,
, ![]()
(3)所求的实数m的取值范围是![]()
解析:
(I)由图可知二次函数的图象过点(0,0),(1,0)
则![]() ,又因为图象过点(2,6)∴6=2a ∴a=3
,又因为图象过点(2,6)∴6=2a ∴a=3
∴函数![]() 的解析式为
的解析式为![]() ………3分
………3分
(Ⅱ)由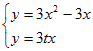 得
得
![]()
∵![]() ,∴直线
,∴直线![]() 与
与![]() 的图象的交点横坐标分别为0,1+t ,
的图象的交点横坐标分别为0,1+t ,
……………5分
由定积分的几何意义知:
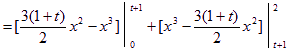
![]()
![]() ,
, ![]() ……………8分
……………8分
(III)∵曲线方程为![]() ,
,![]() ,∴
,∴![]() ,
,
∴点![]() 不在曲线上。设切点为
不在曲线上。设切点为![]() ,则点M的坐标满足
,则点M的坐标满足
![]() ,因
,因![]() ,故切线的斜率为
,故切线的斜率为
![]() ,整理得
,整理得![]() .
.
∵过点![]() 可作曲线的三条切线,
可作曲线的三条切线,
∴关于x0方程![]() 有三个实根. ……………12分
有三个实根. ……………12分
设![]() ,则
,则![]() ,由
,由![]() 得
得![]()
∵当![]() ∴
∴![]() 在
在![]() 上单调递增,
上单调递增,
∵当![]() ,∴
,∴![]() 在
在![]() 上单调递减.
上单调递减.
∴函数![]() 的极值点为
的极值点为![]() ,
,
∴关于x0方程![]() 有三个实根的充要条件是
有三个实根的充要条件是![]() ,
,
解得![]() ,故所求的实数m的取值范围是
,故所求的实数m的取值范围是![]() 。 ………15分
。 ………15分

练习册系列答案
相关题目
 如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.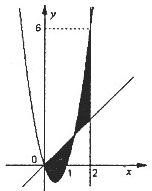 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.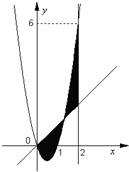 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.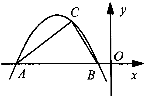 如图,已知二次函数y=ax2+bx+c(a,b,c为实数,a≠0)的图象过点C(t,2),且与x轴交于A,B两点,若AC⊥BC,则a的值为
如图,已知二次函数y=ax2+bx+c(a,b,c为实数,a≠0)的图象过点C(t,2),且与x轴交于A,B两点,若AC⊥BC,则a的值为