题目内容
设函数 ,则( )
,则( )
A. 为 为 的极大值点 的极大值点 | B. 为 为 的极小值点 的极小值点 |
C. 为 为 的极大值点 的极大值点 | D. 为 为 的极小值点 的极小值点 |
B
解析试题分析: ,则当
,则当 时,函数为增函数,当
时,函数为增函数,当 时为减函数,当
时为减函数,当 时为增函数,当
时为增函数,当 时,函数为减函数.又
时,函数为减函数.又 ,故
,故 为
为 的极小值点.
的极小值点.
考点:函数的极值.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
有一段“三段论”推理是这样的:“对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点;因为函数
的极值点;因为函数 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数 的极值点.”以上推理中( )
的极值点.”以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
若 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A. | B. | C. | D.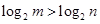 |
用二分法求方程 的近似解,可以取的一个区间是( )
的近似解,可以取的一个区间是( )
A. | B. | C.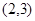 | D. |
定义在区间 的奇函数
的奇函数 为增函数,偶函数
为增函数,偶函数 在区间
在区间 的图象与
的图象与 的图象重合,设
的图象重合,设 ,给出下列不等式:
,给出下列不等式:
①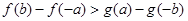 ②
②
③ ④
④ 其中成立的是( )
其中成立的是( )
| A.①与④ | B.②与③ | C.①与③ | D.②与④ |
下列函数中,既是偶函数又在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
方程 的正实根个数为( )
的正实根个数为( )
| A.2个 | B.3个 | C.4个 | D.无数个 |
函数 的定义域为( )
的定义域为( )
A.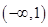 |
B. |
C. |
D.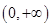 |

 的部分图像可能是( )
的部分图像可能是( )