题目内容
设函数f(x)=x2,g(x)=alnx+bx(a>0).(1)若f(1)=g(1),f′(1)=g′(1),求F(x)=f(x)-g(x)的极小值;
(2)在(1)的结论下,是否存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m成立?若存在,求出k和m,若不存在,说明理由.
【答案】分析:(1)由函数解析式,求出导函数的解析式,根据f(1)=g(1),f'(1)=g'(1),可求出a,b的值,进而求出F(x)的解析式,求导后,分析函数的单调性,进而可得F(x)的极小值
(2)根据(1)可得(1,1)是f(x)和g(x)的公共点,过此点两个函数图象的公切线为y=2x-1,若存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m成立,即f(x)≥2x-1和g(x)≤2x-1同时成立,根据二次函数的图象和性质及导数法判断后可得答案.
解答:解:(1)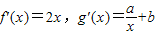 ,代入可得:a=1,b=1
,代入可得:a=1,b=1
∴F(x)=x2-lnx-x,
∴ =
= =
=
∵当x∈(0,1)时,F′(x)<0,当x∈(1,+∞)时,F′(x)>0,
∴F(x)在(0,1)递减,(1,+∞)递增,
∴F(x)的极小值为F(1)=0
(2)由(1)得,(1,1)是f(x)和g(x)的公共点,
f(x)在点(1,1)处的切线方程是y=2x-1
∴若存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m成立
即f(x)≥2x-1和g(x)≤2x-1同时成立
∵f(x)-2x+1=x2-2x+1=(x-1)2≥0,
∴f(x)≥2x-1
令h(x)=g(x)-2x+1, ,
,
∴h(x) 在(0,1)递增,(1,+∞)递减,
∴h(x)max=h(1)=0,
∴h(x)≤0,即g(x)≤2x-1成立
∴存在k=2,m=-1使得f(x)≥kx+m和g(x)≤kx+m成立
点评:本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数的单调性,其中(1)中求出a,b值,进而确定函数的解析式是解答的关键.
(2)根据(1)可得(1,1)是f(x)和g(x)的公共点,过此点两个函数图象的公切线为y=2x-1,若存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m成立,即f(x)≥2x-1和g(x)≤2x-1同时成立,根据二次函数的图象和性质及导数法判断后可得答案.
解答:解:(1)
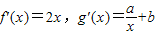 ,代入可得:a=1,b=1
,代入可得:a=1,b=1∴F(x)=x2-lnx-x,
∴
 =
= =
=
∵当x∈(0,1)时,F′(x)<0,当x∈(1,+∞)时,F′(x)>0,
∴F(x)在(0,1)递减,(1,+∞)递增,
∴F(x)的极小值为F(1)=0
(2)由(1)得,(1,1)是f(x)和g(x)的公共点,
f(x)在点(1,1)处的切线方程是y=2x-1
∴若存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m成立
即f(x)≥2x-1和g(x)≤2x-1同时成立
∵f(x)-2x+1=x2-2x+1=(x-1)2≥0,
∴f(x)≥2x-1
令h(x)=g(x)-2x+1,
 ,
,∴h(x) 在(0,1)递增,(1,+∞)递减,
∴h(x)max=h(1)=0,
∴h(x)≤0,即g(x)≤2x-1成立
∴存在k=2,m=-1使得f(x)≥kx+m和g(x)≤kx+m成立
点评:本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数的单调性,其中(1)中求出a,b值,进而确定函数的解析式是解答的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目