题目内容
在△ABC中,角A、B、C所对的边分别为a,b,c,且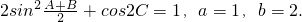
(1)求C和c.
(2)P为△ABC内任一点(含边界),点P到三边距离之和为d,设P到AB,BC距离分别为x,y,用x,y表示d并求d的取值范围.
 解:(1)∵
解:(1)∵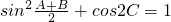
∴
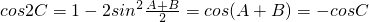
∴2cos2C+cosC-1=0
∴
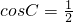 或-1
或-1∵
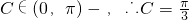
由余弦定理
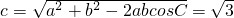
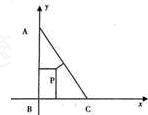
(2)由(1)知△ABC是直角三角形,如图建立直角坐标系,
直线AC的方程为
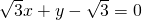 ,
,设P(x,y),
则
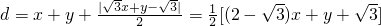
又x,y满足
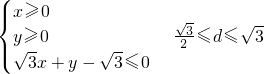
分析:(1)利用二倍角公式对题设等式化简整理得关于cosC的一元二次方程求得cosC的值,进而求得C,进而通过余弦定理求得c.
(2)根据三边的长可知此三角形为直角三角形,进而以两直角边为坐标轴建立直角坐标系,则可推断出AC的直线方程,设出P的坐标,则可用x和y和点P到直线AC的距离表示出P到三边的距离,进而根据题意可判断出x和y满足的不等式关系,进而求得d的范围.
点评:本题主要考查了解三角形的实际应用.涉及了三角函数中的二倍角公式,余弦定理和点到直线的距离公式等.考查了基础知识的综合运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |