题目内容
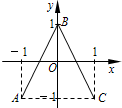 (2013•浙江模拟)如图,函数y=f(x)的图象为折线ABC,设g (x)=f[f(x)],则函数y=g(x)的图象为( )
(2013•浙江模拟)如图,函数y=f(x)的图象为折线ABC,设g (x)=f[f(x)],则函数y=g(x)的图象为( )分析:函数y=f(x)的图象为折线ABC,其为偶函数,所研究x≥0时g(x)的图象即可,首先根据图象求出x≥0时f(x)的图象及其值域,再根据分段函数的性质进行求解,可以求出g(x)的解析式再进行判断;
解答:解:如图:函数y=f(x)的图象为折线ABC,函数f(x)为偶函数,
我们可以研究x≥0的情况即可,
若x≥0,可得B(0,1),C(1,-1),这直线BC的方程为:lBC:y=-2x+1,x∈[0,1],其中-1≤f(x)≤1;
若x<0,可得lAB:y=2x+1,∴f(x)=
,
我们讨论x≥0的情况:如果0≤x≤
,解得0≤f(x)≤1,此时g(x)=f[f(x)]=-2(-2x+1)=4x-1;
若
<x≤1,解得-1≤f(x)<0,此时g(x)=f[f(x)]=2(-2x+1)=-4x+3;
∴x∈[0,1]时,g(x)=
;
故选A;
我们可以研究x≥0的情况即可,
若x≥0,可得B(0,1),C(1,-1),这直线BC的方程为:lBC:y=-2x+1,x∈[0,1],其中-1≤f(x)≤1;
若x<0,可得lAB:y=2x+1,∴f(x)=
|
我们讨论x≥0的情况:如果0≤x≤
| 1 |
| 2 |
若
| 1 |
| 2 |
∴x∈[0,1]时,g(x)=
|
故选A;
点评:此题主要考查分段函数的定义域和值域以及复合函数的解析式求法,是一道好题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•浙江模拟)函数f(x)=Asin(ωx+φ)(A>0,ω>),|φ|<
(2013•浙江模拟)函数f(x)=Asin(ωx+φ)(A>0,ω>),|φ|< (2013•浙江模拟)如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若|
(2013•浙江模拟)如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若|