题目内容
已知α是三角形的内角,且sinα+cosα=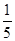 .
.
(1)求tanα的值;
(2)将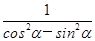 用tanα表示出来,并求其值.
用tanα表示出来,并求其值.
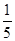 .
.(1)求tanα的值;
(2)将
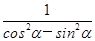 用tanα表示出来,并求其值.
用tanα表示出来,并求其值.(1)-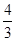 (2)
(2)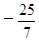
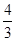 (2)
(2)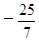
(1)(解法1)联立方程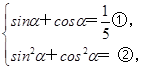 由①得cosα=
由①得cosα=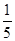 -sinα,
-sinα,
将其代入②,整理,得25sin2α-5sinα-12=0.
∵α是三角形内角,∴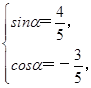 ∴tanα=-
∴tanα=-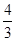 .
.
(解法2)∵sinα+cosα=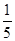 ,∴(sinα+cosα)2=
,∴(sinα+cosα)2=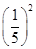 ,即1+2sinαcosα=
,即1+2sinαcosα=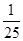 ,
,
∴2sinαcosα=-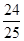 ,∴(sinα-cosα)2=1-2sinαcosα=1+
,∴(sinα-cosα)2=1-2sinαcosα=1+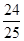 =
=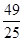 .
.
∵sinαcosα=-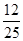 <0且0<α<π,∴sinα>0,cosα<0.
<0且0<α<π,∴sinα>0,cosα<0.
∵sinα-cosα>0,∴sinα-cosα=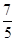 .
.
由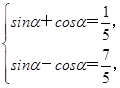 得
得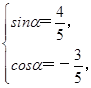 ∴tanα=-
∴tanα=-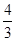 .
.
(2)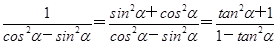 .
.
∵tanα=-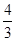 ,∴
,∴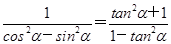 =
=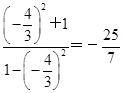 .
.
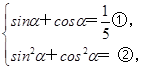 由①得cosα=
由①得cosα=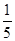 -sinα,
-sinα,将其代入②,整理,得25sin2α-5sinα-12=0.
∵α是三角形内角,∴
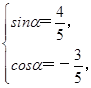 ∴tanα=-
∴tanα=-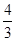 .
.(解法2)∵sinα+cosα=
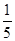 ,∴(sinα+cosα)2=
,∴(sinα+cosα)2=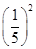 ,即1+2sinαcosα=
,即1+2sinαcosα=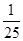 ,
,∴2sinαcosα=-
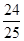 ,∴(sinα-cosα)2=1-2sinαcosα=1+
,∴(sinα-cosα)2=1-2sinαcosα=1+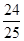 =
=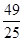 .
.∵sinαcosα=-
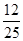 <0且0<α<π,∴sinα>0,cosα<0.
<0且0<α<π,∴sinα>0,cosα<0.∵sinα-cosα>0,∴sinα-cosα=
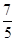 .
.由
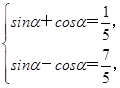 得
得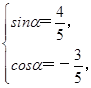 ∴tanα=-
∴tanα=-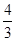 .
.(2)
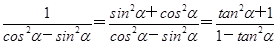 .
.∵tanα=-
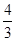 ,∴
,∴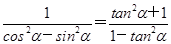 =
=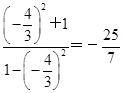 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
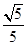 ,sinβ=
,sinβ=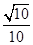 ,且α、β均为锐角,求α+β的值.
,且α、β均为锐角,求α+β的值.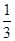 ,
,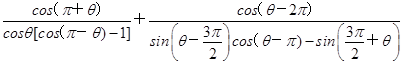 的值.
的值.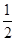 ,且角α在第四象限,计算:
,且角α在第四象限,计算: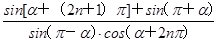 (n∈Z).
(n∈Z). ,则sinα=________.
,则sinα=________.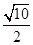 ,则tan 2α=( )
,则tan 2α=( )

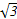 =
=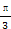



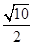 ,则tan 2α等于________.
,则tan 2α等于________. ,则
,则 的值为_______________.
的值为_______________.