题目内容
若不等式|x-a|＜1成立的充分非必要条件是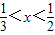
则实数a的取值范围是（ ）A．
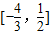
B．
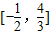
C．
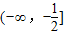
D．
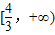
【答案】分析：首先算出|x-a|＜1的解，即a-1＜x＜a+1．由题意说明，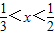
是a-1＜x＜a+1的真子集，求解即可．
解答：解：由|x-a|＜1，可得a-1＜x＜a+1．
它的充分非必要条件是
＜x＜
，
也就是说
＜x＜
是a-1＜x＜a+1的真子集，则a须满足属于{a|a-1≤
且a+1＞
}或{a|a-1＜
且a+1≥
}；
解得a∈（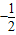
，
]∪[
，
），
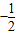即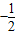
≤a≤
故选B．
点评：本题考查绝对值不等式的解法，必要条件、充分条件与充要条件的判断，考查计算能力，是中档题．
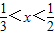是a-1＜x＜a+1的真子集，求解即可．解答：解：由|x-a|＜1，可得a-1＜x＜a+1．
它的充分非必要条件是
＜x＜，也就是说
＜x＜是a-1＜x＜a+1的真子集，则a须满足属于{a|a-1≤且a+1＞}或{a|a-1＜且a+1≥}；解得a∈（
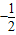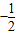，]∪[，），即
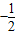≤a≤故选B．
点评：本题考查绝对值不等式的解法，必要条件、充分条件与充要条件的判断，考查计算能力，是中档题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目