题目内容
（2009•奉贤区一模）已知函数f(x)=| 6 |
| x2+1 |
（1）在直角坐标系中，画出函数f(x)=
| 6 |
| x2+1 |
（2）关于x的不等式f（x）≥k-7x2的解集一切实数，求实数k的取值范围；
（3）关于x的不等式f(x)＞
| a |
| x |
分析：（1）图象特征大致是过点（0，6）定义域R的偶函数，值域（0，6]，在（0，+∞）单调递减区间，然后画图大致图象即可；
（2）解法一：依题意，将k分离出来，然后利用函数的单调性研究不等式另一侧函数的最小值，从而求出k的范围；
解法二：7x4+（7-k）x2+6-k≥0对一切实数恒成立，设x2=t≥0，可转化成函数h（t）=7t2+（7-k）t+6-k（t≥0）的最小值大于等于0恒成立，建立关系式，解之即可；
（3）方法一：依题意有a＞0，所对应方程有两个同号的正根，然后根据韦达定理可知必有一个小的根x1∈（0，1）则x2∈（3，4]，利用求根公式建立关系式，解之即可；
方法二：依题意有a＞0，不等式
＞
(x+
)的解集（x1，x2），根据函数y=x+
(x＞0)的性质知道：其中x1∈（0，1）x2∈（3，4]，然后建立关系式，解之即可；
方法三：依题意有a＞0，不等式a＜
的解集（x1，x2），根据函数y=
(x＞0)的性质知道：其中x1∈（0，1）x2∈（3，4]，然后建立关系式，解之即可；
方法四：数形结合，依题意有a＞0，画出符合题意的大致图形，交点的横坐标是方程x2-
x+6=0的解，然后建立关系式，解之即可．
（2）解法一：依题意，将k分离出来，然后利用函数的单调性研究不等式另一侧函数的最小值，从而求出k的范围；
解法二：7x4+（7-k）x2+6-k≥0对一切实数恒成立，设x2=t≥0，可转化成函数h（t）=7t2+（7-k）t+6-k（t≥0）的最小值大于等于0恒成立，建立关系式，解之即可；
（3）方法一：依题意有a＞0，所对应方程有两个同号的正根，然后根据韦达定理可知必有一个小的根x1∈（0，1）则x2∈（3，4]，利用求根公式建立关系式，解之即可；
方法二：依题意有a＞0，不等式
| 1 |
| a |
| 1 |
| 6 |
| 1 |
| x |
| 1 |
| x |
方法三：依题意有a＞0，不等式a＜
| 6x |
| x2+1 |
| 6x |
| x2+1 |
方法四：数形结合，依题意有a＞0，画出符合题意的大致图形，交点的横坐标是方程x2-
| 6 |
| a |
解答：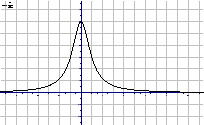
（理）
解：（1）图象特征大致如下，过点（0，6）定义域R的偶函数，
值域（0，6]，在（0，+∞）单调递减区间
（2）解法一：依题意，变形为k≤
+7x2对一切实数x∈R恒成立（1分）k≤
+7(x2+1)-7，设h(x)=
+7(x2+1)-7，k≤h（x）min（1分）
h(x)=
+7(x2+1)-7在[0，+∞）单调递减（可用函数单调性定义证明或复合函数的单调性说明）（4分
h（x）min=h（0）=6∴k≤6（1分）
解法二：6≥（k-7x2）（x2+1），7x4+（7-k）x2+6-k≥0对一切实数恒成立（1分）
设x2=t≥0，h（t）=7t2+（7-k）t+6-k（t≥0）的最小值大于等于0恒成立（1分）；
∴k≤6（2分）
∴k∈Φ（2分）∴k≤6（1分）
（3）方法一：依题意有a＞0（1分）
不等式变形为ax2-6x+a＜0，x2-
x+1＜0当△=
-4≤0时不合题意，舍去 （1分）△＞0时a2＜9，∴0＜a＜3（1分）
方程x2-
x+1=0的有两根x1，x2（x1＜x2）∵x1x2=1，x1+x2=
＞2，方程有两个同号的正根，且必有一个小的根x1∈（0，1）∴x2∈（3，4]，（2分）∴3＜
≤4，（1分）
解得不等式
≤a＜
（1分）
方法二：依题意有a＞0，（1分）
不等式
＞
(x+
)的解集（x1，x2），（1分）
根据函数y=x+
(x＞0)的性质知道：其中x1∈（0，1）x2∈（3，4]，（2分）
∴
(3+
)＜
≤
(4+
)（1分）
所以
≤a＜
（2分）
方法三：依题意有a＞0，（1分）
不等式a＜
的解集（x1，x2），（1分）
根据函数y=
(x＞0)的性质知道：其中x1∈（0，1）x2∈（3，4]，（2分）
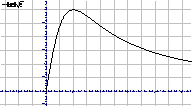
（1分）
所以
≤a＜
（2分）
方法四数形结合
依题意有a＞0，（1分）
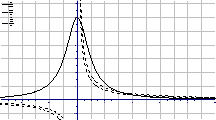画出符合题意的大致图形
交点的横坐标是方程x2-
x+6=0的解（2分）x2=4=
=4，a=
x2=4=
=3，a=
（2分）
所以
≤a＜
（2分）
（理）解：（1）图象特征大致如下，过点（0，6）定义域R的偶函数，
值域（0，6]，在（0，+∞）单调递减区间
（2）解法一：依题意，变形为k≤
| 6 |
| x2+1 |
| 6 |
| x2+1 |
| 6 |
| x2+1 |
h(x)=
| 6 |
| x2+1 |
h（x）min=h（0）=6∴k≤6（1分）
解法二：6≥（k-7x2）（x2+1），7x4+（7-k）x2+6-k≥0对一切实数恒成立（1分）
设x2=t≥0，h（t）=7t2+（7-k）t+6-k（t≥0）的最小值大于等于0恒成立（1分）；
|
|
（3）方法一：依题意有a＞0（1分）
不等式变形为ax2-6x+a＜0，x2-
| 6 |
| a |
| 36 |
| a2 |
方程x2-
| 6 |
| a |
| 6 |
| a |
6+
| ||
| 2a |
解得不等式
| 24 |
| 17 |
| 9 |
| 5 |
方法二：依题意有a＞0，（1分）
不等式
| 1 |
| a |
| 1 |
| 6 |
| 1 |
| x |
根据函数y=x+
| 1 |
| x |
∴
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| 6 |
| 1 |
| 4 |
所以
| 24 |
| 17 |
| 9 |
| 5 |
方法三：依题意有a＞0，（1分）
不等式a＜
| 6x |
| x2+1 |
根据函数y=
| 6x |
| x2+1 |
|
所以
| 24 |
| 17 |
| 9 |
| 5 |
方法四数形结合
依题意有a＞0，（1分）
画出符合题意的大致图形交点的横坐标是方程x2-
| 6 |
| a |
6+
| ||
| 2a |
| 24 |
| 17 |
6+
| ||
| 2a |
| 9 |
| 5 |
所以
| 24 |
| 17 |
| 9 |
| 5 |
点评：本题主要考查了一元二次不等式的应用，以及不等式恒成立问题，同时考查了数形结合，利用函数单调性求函数的最值等有关问题，属于中档题．
练习册系列答案
相关题目