题目内容
从直线x-y+3=0上的点向圆x2+y2-4x-4y+7=0引切线,则切线长的最小值为
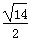
解析试题分析:把圆的方程化为标准式后,找出圆心坐标和圆的半径,利用图形可知,当圆心A与直线x-y+3=0垂直时,过垂足作圆的切线,切线长最短,连接AB,根据圆的切线垂直于过切点的直径可得三角形ABC为直角三角形,利用点到直线的距离公式求出圆心到直线x-y+3=0的距离即为|AC|的长,然后根据半径和|AC|的长,利用勾股定理即可求出此时的切线长.由于圆心(2,2),半径为1,那么可知圆心到直线的距离为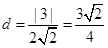 ,那么利用勾股定理可知切线长的最小值为
,那么利用勾股定理可知切线长的最小值为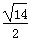 。
。
考点:圆的切线
点评:此题考查学生学生灵活运用点到直线的距离公式化简求值,掌握圆的切线垂直于过切点的直径这个性质,是一道中档题.此题的关键是找出切线长最短时的条件,根据题意画出相应的图形

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
 的棱长为2,点
的棱长为2,点 是
是 的中点,点
的中点,点 是正方形
是正方形 所在平面内的一个动点,且满足
所在平面内的一个动点,且满足 ,
, 的距离为
的距离为 ,则点
,则点 ,当竹竿滑动到A1B1位置时,
,当竹竿滑动到A1B1位置时, ,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
 的最小值为 .
的最小值为 .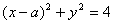 的圆心坐标为
的圆心坐标为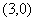 ,则实数
,则实数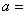 .
.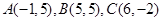 的圆的方程是 .
的圆的方程是 .  中,直线的参数方程为
中,直线的参数方程为 (t为参数);在极坐标系(与直
(t为参数);在极坐标系(与直 为极点,以
为极点,以 的正半轴为极轴)中,圆的极坐标方
的正半轴为极轴)中,圆的极坐标方 ,则此直线与此圆的位置关系是 .
,则此直线与此圆的位置关系是 . ,过点
,过点 作直线交圆C于
作直线交圆C于 两点,
两点, 面积的最大值为__________.
面积的最大值为__________. 是直角三角形的三边(
是直角三角形的三边( 为斜边), 则圆
为斜边), 则圆 被直线
被直线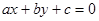 所截得的弦长等于__________.
所截得的弦长等于__________.