题目内容
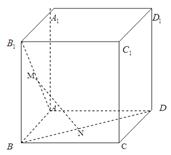
如图在棱长为1的正方体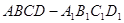 中,M,N分别是线段
中,M,N分别是线段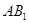 和BD上的点,且AM=BN=
和BD上的点,且AM=BN=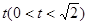
(1)求|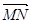 |的最小值;
|的最小值;
(2)当|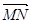 |达到最小值时,
|达到最小值时,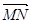 与
与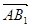 ,
,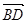 是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.
是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.
【答案】
(1) ;(2)垂直,详见解析.
;(2)垂直,详见解析.
【解析】
试题分析:(1)作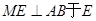 ,连
,连 .易知
.易知 ,再由余弦定理可得:
,再由余弦定理可得: ,则
,则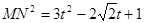 ,根据二次函数的知识即可得到其最小值;建立空间直角坐标系,利用空间向量方法,写出
,根据二次函数的知识即可得到其最小值;建立空间直角坐标系,利用空间向量方法,写出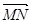 ,
, ,
, 的坐标,利用数量积即可求证它们是否垂直.
的坐标,利用数量积即可求证它们是否垂直.
试题解析:(1)作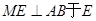 ,连
,连 .易知
.易知
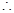 在
在 ,由余弦定理可得:
,由余弦定理可得: 
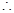 在
在 ,
,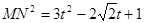 。当
。当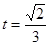 时,
时, 最小值=
最小值= .
.
(2)以点 为坐标原点,以
为坐标原点,以 所在的直线分别为
所在的直线分别为 轴建立直角坐标系,由(1)可知,
轴建立直角坐标系,由(1)可知,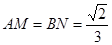 ,所以点
,所以点 ,
,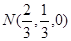 ,
,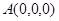 ,
, ,
,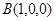 ,
,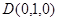 ,
,
则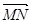
 ,
,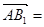
 ,
,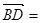
 ,
,
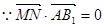 ,
,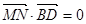
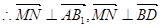
即当|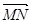 |达到最小值时,
|达到最小值时,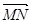 与
与 ,
, 是否都垂直.
是否都垂直.
考点:本题主要考查了立体几何中的向量方法,以及运算能力和推理论证能力,属于基础题..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
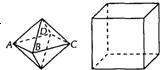
 (2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )
(2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )

