题目内容
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有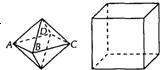
分析:正四棱锥的底面是正方形ABCD,过ABCD的平面与正方体的某一个平面平行的截面也是正方形,
当ABCD在截面内转动时,会有无数个正方形,所以几何体有无数个.
当ABCD在截面内转动时,会有无数个正方形,所以几何体有无数个.
解答:解:(法一):本题可以转化为一个正方形可以有多少个内接正方形,显然有无穷多个.
(法二):通过计算,显然两个正四校锥的高均为
,考查放入正方体后,面ABCD所在的截面,显然其面积是不固定的,取值范围是:[
,1),所以该儿何体的体积取值范围是:[
,
].
(法二):通过计算,显然两个正四校锥的高均为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
点评:本通主要考查学生能否迅速构出一些常见的几何模型,并不是以计算为主.

练习册系列答案
相关题目



 两个相同的正四棱锥组成如图所示的几何体,可放入棱
两个相同的正四棱锥组成如图所示的几何体,可放入棱 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为