Question

已知定义在R上的函数f（x）的图象是连续不断的，且有如下部分对应值表：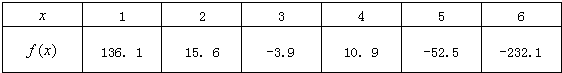
判断函数的零点个数至少有

1. A.
   2个
2. B.
   3个
3. C.
   4个
4. D.
   5个

Answer 1

B
分析：由f（2）•f（3）＜0，f（3）•f（4）＜0，f（4）•f（5）＜0 知，f（x）在区间[2，3]、[3，4]、[4，5]上都至少存在一个零点，综合可得答案．
解答：∵函数f（x）的图象是连续不断的，
由图表知，f（2）•f（3）＜0，f（3）•f（4）＜0，f（4）•f（5）＜0，
∴函数f（x）在区间[2，3]、[3，4]、[4，5]上都至少存在一个零点，
∴函数f（x）在区间[1，6]上的零点至少有3个零点，
故选B．
点评：本题考查函数零点存在的条件，若连续函数在一个区间[a，b]的端点函数值f（a）f（b）＜0，则函数在此区间内至少存在一个零点．