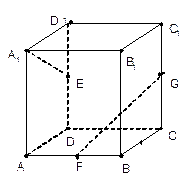题目内容
已知二面角α-l-β的大小为50°,P为空间中任意一点,则过点P且与平面α和平面β所成的角都是25°的直线的条数为( )
| A.2 | B.3 | C. 4 | D.5 |
B
分析:利用线面角的概念及角平分线的性质,分析出所求直线二面角的平分面上,再根据线面角的大小变化确定出直线条数.
解:首先给出下面两个结论
①两条平行线与同一个平面所成的角相等.
②与二面角的两个面成等角的直线在二面角的平分面上.
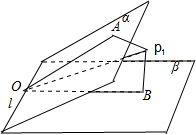 图1.
图1.(1)如图1,过二面角α-l-β内任一点作棱l的垂面AOB,交棱于点O,与两半平面于OA,OB,则∠AOB为二面角α-l-β的平面角,∠AOB=50°
设OP1为∠AOB的平分线,则∠P1OA=∠P1OB=25°,与平面α,β所成的角都是25°,此时过P且与OP1平行的直线符合要求,有一条.当OP1以O为轴心,在二面角α-l-β的平分面上转动时,OP1与两平面夹角变小,不再会出现25°情形.
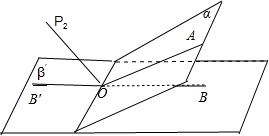 图2.
图2.(2)如图2,设OP2为∠AOB的补角∠AOB′,则∠P2OA=∠P2OB=65°,与平面α,β所成的角都是65°.当OP2以O为轴心,在二面角α-l-β′的平分面上转动时,OP2与两平面夹角变小,对称地在图中OP2两侧会出现25°情形,有两条.此时过P且与OP2平行的直线符合要求,有两条.
综上所述,直线的条数共有三条.
故选B.

练习册系列答案
相关题目
 是以BC为斜边的直角三角形,则实数x的值为 。
是以BC为斜边的直角三角形,则实数x的值为 。 与向量
与向量 平行,则
平行,则 __
__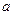 ,且正方体各面的中心是一个几何体的顶点,求这个几何体的棱长.
,且正方体各面的中心是一个几何体的顶点,求这个几何体的棱长.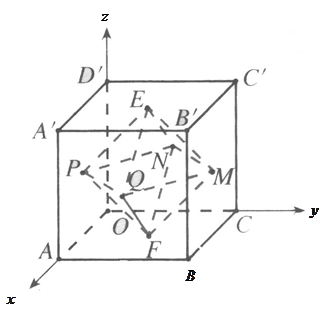
 =(2,-1,3),
=(2,-1,3), =(-1,4,-2),
=(-1,4,-2), =(7,5,λ),若
=(7,5,λ),若



 中,点
中,点 为上底面
为上底面 的中点,
的中点, ,则
,则 的值分别是( )
的值分别是( )



 =(1,1,x),
=(1,1,x),  =(1,2,1),
=(1,2,1),  =(1,1,1),满足条件
=(1,1,1),满足条件 =―
=― =( )
=( )

 中,AA1=AB=4,AD=2,
中,AA1=AB=4,AD=2,