题目内容
已知函数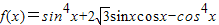
(1)将函数化为
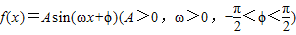 的形式,并写出最小正周期.
的形式,并写出最小正周期.(2)用“五点法”作函数的图象,并写出该函数在[0,π]的单调递增区间

(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,求x1+x2.
【答案】分析:(1) 利用二倍角公式、两角差的正弦公式化简函数的解析式,求出最小正周期.
(2) 根据函数的解析式,用五点法做出简图,结合图象求出在[0,π]上的单调增区间.
(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,由图象的对称性知,x1,x2关于对称轴x=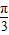 对称,从而有
对称,从而有 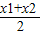 =
=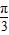 .
.
解答:解:(1)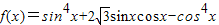 =sin2x-cos2x+
=sin2x-cos2x+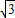 sin2x=
sin2x=
2(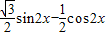 )=2sin(2x-
)=2sin(2x-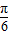 ).最小正周期为 T=
).最小正周期为 T=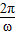 =π.
=π.
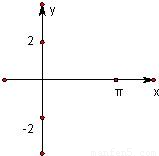
(2) 用五点法做出简图,列表如下:
描点作图: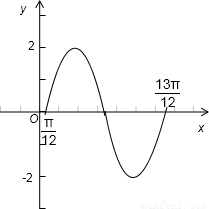
在[0,π]上的单调增区间为[0,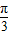 ],[
],[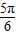 ,π].
,π].
(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,由图象的对称性知,
x1,x2关于对称轴 x=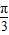 对称,故
对称,故 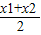 =
=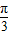 ,∴x1+x2=
,∴x1+x2=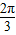 .
.
点评:本题考查三角公式的应用,用五点法作图,正弦函数的图象和性质,体现了数形结合的数学思想,作图是解题的难点.
(2) 根据函数的解析式,用五点法做出简图,结合图象求出在[0,π]上的单调增区间.
(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,由图象的对称性知,x1,x2关于对称轴x=
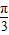 对称,从而有
对称,从而有 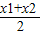 =
=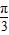 .
.解答:解:(1)
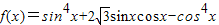 =sin2x-cos2x+
=sin2x-cos2x+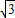 sin2x=
sin2x=2(
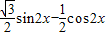 )=2sin(2x-
)=2sin(2x-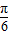 ).最小正周期为 T=
).最小正周期为 T=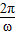 =π.
=π.(2) 用五点法做出简图,列表如下:
2x-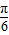 | 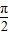 | π | 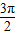 | 2 π | |
| x | 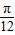 | 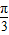 | 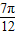 | 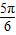 | 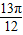 |
| y | 2 | -2 |

在[0,π]上的单调增区间为[0,
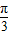 ],[
],[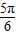 ,π].
,π].(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,由图象的对称性知,
x1,x2关于对称轴 x=
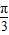 对称,故
对称,故 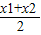 =
=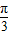 ,∴x1+x2=
,∴x1+x2=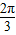 .
.点评:本题考查三角公式的应用,用五点法作图,正弦函数的图象和性质,体现了数形结合的数学思想,作图是解题的难点.

练习册系列答案
相关题目
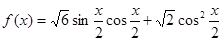
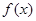 化简成
化简成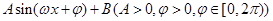 的形式;
的形式;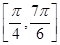 上的最大值和最小值.
上的最大值和最小值.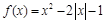 .(1)将函数
.(1)将函数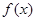 的解析式写成分段函数;
的解析式写成分段函数;