Question

已知平面α⊥平面β，交线为AB，C∈α，D∈β，AB＝AC＝BC＝4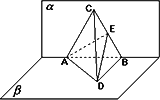，E为BC的中点，AC⊥BD，BD＝8．

①求证：BD⊥平面α；

②求证：平面AED⊥平面BCD；

③求二面角B－AC－D的正切值．

Answer 1

答案：
解析：

解析：①AB是AC在平面β上的射影，由AC⊥BD得AB⊥BD．∵α⊥β．∴DB⊥α． 　　②由AB＝AC，且E是BC中点，得AE⊥BC，又AE⊥DB，故AE⊥平面BCD，因此可证得平面AED⊥平面BCD． 　　③设F是AC中点，连BF，DF．由于△ABC是正三角形，故BF⊥AC．又由DB⊥平面α，则DF⊥AC，∠BFD是二面角B－AC－D的平面角， 　　在Rt△BFD中，．