题目内容
4.双曲线$\frac{{y}^{2}}{{b}^{2}}$-$\frac{{x}^{2}}{{a}^{2}}$=1(a>0,b>0)的一条渐近线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)交于点M、N,则|MN|等于$\sqrt{2({a}^{2}+{b}^{2})}$.分析 求出双曲线的渐近线方程,将渐近线方程与椭圆的方程联立,求出两个交点的坐标;利用两点的距离公式求出|MN|.
解答 解:不妨取双曲线的渐近线的方程为y=$\frac{b}{a}$x,
与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1联立消去y得2x2=a2
解得x=±$\frac{\sqrt{2}}{2}$a代入渐近线方程得M,N两点的坐标分别为:($\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$b),(-$\frac{\sqrt{2}}{2}$a,-$\frac{\sqrt{2}}{2}$b),
所以|MN|=$\sqrt{(\sqrt{2}a)^{2}+(\sqrt{2}b)^{2}}$=$\sqrt{2({a}^{2}+{b}^{2})}$.
故答案为:$\sqrt{2({a}^{2}+{b}^{2})}$.
点评 本题考查双曲线的渐近线方程与双曲线的焦点位置有关、考查解决直线与圆锥曲线的位置关系问题,常将直线方程与圆锥曲线方程联立.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
12.(ax+$\frac{1}{x}$)(2x-1)5的展开式中各项系数的和为2,则a的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.若直线a∥α,直线b∥α,则a与b( )
| A. | 平行 | B. | 异面 | C. | 平行或异面 | D. | 相交、平行或异面 |
16.在侧棱长为2$\sqrt{3}$的正三棱锥S-ABC中,∠ASB=∠BSC=∠CSA=40°,过A作截面AMN,则截面的最小周长为( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 6 | D. | 10 |
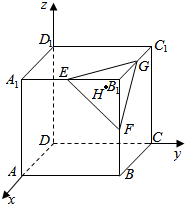 如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.
如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.