题目内容
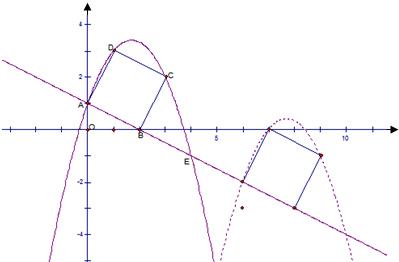
如图,直线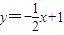 交坐标轴于A、B两点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B两点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.(1)求抛物线的解析式.
(2)若正方形以每秒
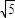 个单位长度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间的函数关系式,并写出自变量的取值范围.
个单位长度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间的函数关系式,并写出自变量的取值范围.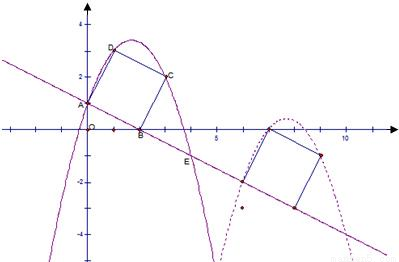
【答案】分析:(1)可先根据AB所在直线的解析式求出A,B两点的坐标,即可得出OA、OB的长.过D作DM⊥y轴于M,则△ADM≌△BAO,由此可得出MD、MA的长,也就能求出D的坐标,同理可求出C的坐标;可根据A、C、D三点的坐标,用待定系数法求出抛物线的解析式;
(2)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当A′在x轴下方,但C′在x轴上方或x轴上时,即当1<t≤2时,S为梯形A′GB′H的面积,可参照①的方法求出A′G和B′H的长,那么梯形的上下底就可求出,梯形的高为A′B′即正方形的边长,可根据梯形的面积计算公式得出关于S、t的函数关系式.
③当D′逐渐移动到x轴的过程中,即当2<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
解答:解:(1)(2)设抛物线为y=ax2+bx+c,抛物线过(0,1)(3,2)(1,3),
∴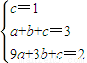
解得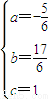
∴抛物线方程为y=- x2+
x2+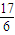 x+1,.
x+1,.
(2)①当点A运动到点F时,t=1,
当0<t≤1时,
∵∠OFA=∠GFB′,
tan∠OFA=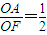 ,
,
∴tan∠GFB′=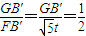 ,
,
∴GB′=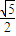 t
t
∴S△FB′G= FB′×GB′
FB′×GB′
= ×
×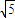 t×
t×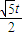 =
= t2;
t2;
②当点C运动到x轴上时,t=2,
当1<t≤2时,如图3,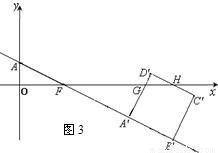
A′B′=AB=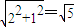 ,
,
∴A′F=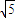 t-
t-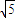 ,
,
∴A′G=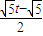 ,
,
∵B′H=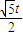 ,
,
∴S梯形A′B′HG= (A′G+B′H)×A′B′
(A′G+B′H)×A′B′
=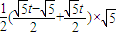 =
= t-
t- ;
;
③当点D运动到x轴上时,t=3,
当2<t≤3时,如图4,
∵A′G=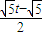 ,
,
∴GD′= ,
,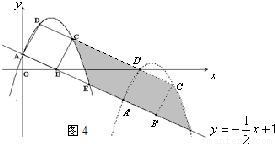
∵S△AOF= ×1×2=1,OA=1,△AOF∽△GD′H
×1×2=1,OA=1,△AOF∽△GD′H
∴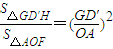 ,
,
∴ ,
,
∴S五边形GA′B′C′H=(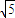 )2-(
)2-(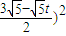
=- t2+
t2+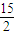 t-
t-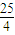 ;(1<t≤2)
;(1<t≤2)
点评:本题着重考查了待定系数法求二次函数解析式、图形平移变换、三角形相似等重要知识点,(3)小题中要根据正方形的不同位置分类进行讨论,不要漏解.
(2)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当A′在x轴下方,但C′在x轴上方或x轴上时,即当1<t≤2时,S为梯形A′GB′H的面积,可参照①的方法求出A′G和B′H的长,那么梯形的上下底就可求出,梯形的高为A′B′即正方形的边长,可根据梯形的面积计算公式得出关于S、t的函数关系式.
③当D′逐渐移动到x轴的过程中,即当2<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
解答:解:(1)(2)设抛物线为y=ax2+bx+c,抛物线过(0,1)(3,2)(1,3),
∴
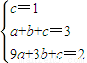
解得
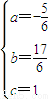
∴抛物线方程为y=-
 x2+
x2+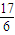 x+1,.
x+1,.(2)①当点A运动到点F时,t=1,
当0<t≤1时,
∵∠OFA=∠GFB′,
tan∠OFA=
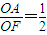 ,
,∴tan∠GFB′=
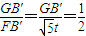 ,
,∴GB′=
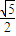 t
t∴S△FB′G=
 FB′×GB′
FB′×GB′=
 ×
×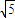 t×
t×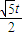 =
= t2;
t2;②当点C运动到x轴上时,t=2,
当1<t≤2时,如图3,

A′B′=AB=
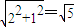 ,
,∴A′F=
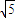 t-
t-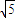 ,
,∴A′G=
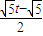 ,
,∵B′H=
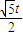 ,
,∴S梯形A′B′HG=
 (A′G+B′H)×A′B′
(A′G+B′H)×A′B′=
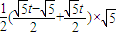 =
= t-
t- ;
;③当点D运动到x轴上时,t=3,
当2<t≤3时,如图4,
∵A′G=
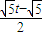 ,
,∴GD′=
 ,
,
∵S△AOF=
 ×1×2=1,OA=1,△AOF∽△GD′H
×1×2=1,OA=1,△AOF∽△GD′H∴
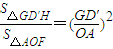 ,
,∴
 ,
,∴S五边形GA′B′C′H=(
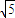 )2-(
)2-(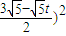
=-
 t2+
t2+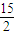 t-
t-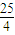 ;(1<t≤2)
;(1<t≤2)点评:本题着重考查了待定系数法求二次函数解析式、图形平移变换、三角形相似等重要知识点,(3)小题中要根据正方形的不同位置分类进行讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线
如图,直线 如图,椭圆的方程为
如图,椭圆的方程为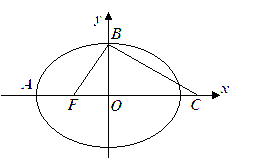
 :
: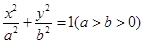 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形. (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线 交椭圆
交椭圆 、
、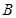 两点,设点
两点,设点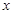 轴的对称点为
轴的对称点为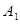 .
.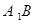 过
过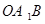 面积的取值范围.
面积的取值范围.