题目内容
如图,点![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 、
、![]() 是椭圆的两个顶点,
是椭圆的两个顶点,
椭圆的离心率为![]() 点
点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() 、
、![]() 、
、![]() 三点确定的圆
三点确定的圆![]() 恰好与直线
恰好与直线![]() 相切.
相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 作一条与两坐标轴都不垂直的直线
作一条与两坐标轴都不垂直的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恰好为△
恰好为△![]() 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
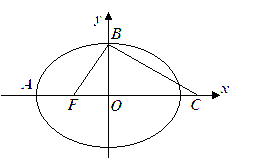
(Ⅰ)![]() (Ⅱ)存在满足条件的定点N,点N的坐标为(
(Ⅱ)存在满足条件的定点N,点N的坐标为(![]() 4,0)
4,0)
解析:
(Ⅰ)由题意可知![]()
![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Ⅱ)假设存在满足条件的点
(Ⅱ)假设存在满足条件的点![]() 由题意可设直线l的方程为
由题意可设直线l的方程为![]()
![]()
![]()
![]()
![]()
![]()
![]()
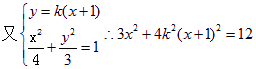
![]()
![]()
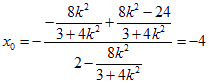
∴存在满足条件的定点N,点N的坐标为(![]() 4,0) ………………14分
4,0) ………………14分

练习册系列答案
相关题目
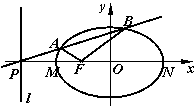
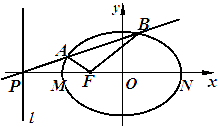 (1)求椭圆的标准方程;(2)求证:对于任意的割线
(1)求椭圆的标准方程;(2)求证:对于任意的割线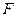 是椭圆
是椭圆 的左焦点,直线
的左焦点,直线 为对应的准线,直线
为对应的准线,直线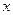 轴交于
轴交于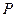 点,
点,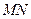 为椭圆的长轴,已知
为椭圆的长轴,已知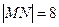 ,且
,且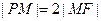 .
.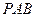 ,恒有
,恒有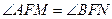 ;
;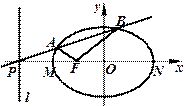
 是椭圆
是椭圆 的左焦点,直线
的左焦点,直线 为对应的准线,直线
为对应的准线,直线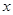 轴交于
轴交于 点,
点, 为椭圆的长轴,已知
为椭圆的长轴,已知 ,且
,且 .
. ,恒有
,恒有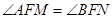 ;
;