题目内容
袋中有分别写着“团团”和“圆圆”的两种玩具共7个且形状完全相同,从中任取2个玩具都是“圆圆”的概率为| 1 | 7 |
(1)求X=4时的概率;
(2)求X的数学期望.
分析:(1)设袋中有玩具“圆圆”n个,根据题意,从中任取2个玩具都是“圆圆”的概率为
,可得
=
,解可得答案;
(2)由题意可知X的可能取值为1,2,3,4,5;分别求出其概率,由期望的公式,计算可得答案.
| 1 |
| 7 |
| ||
|
| 1 |
| 7 |
(2)由题意可知X的可能取值为1,2,3,4,5;分别求出其概率,由期望的公式,计算可得答案.
解答:解:(1)设袋中有玩具“圆圆”n个,
由题意知:
=
,
所以n(n-1)=6,解得n=3(n=-2舍去);
P(X=4)=
=
.
(2)由题意可知X的可能取值为1,2,3,4,5.
∵P(X=1)=
;P(X=2)=
=
;
P(X=3)=
=
;
P(X=4)=
=
;
P(X=5)=
=
,
∴E(X)=1×
+2×
+3×
+4×
+5×
=2.
由题意知:
| ||
|
| 1 |
| 7 |
所以n(n-1)=6,解得n=3(n=-2舍去);
P(X=4)=
| 4×3×2×3 |
| 7×6×5×4 |
| 3 |
| 35 |
(2)由题意可知X的可能取值为1,2,3,4,5.
∵P(X=1)=
| 3 |
| 7 |
| 4×3 |
| 7×6 |
| 2 |
| 7 |
P(X=3)=
| 4×3×3 |
| 7×6×5 |
| 6 |
| 35 |
P(X=4)=
| 4×3×2×3 |
| 7×6×5×4 |
| 3 |
| 35 |
P(X=5)=
| 4×3×2×1×3 |
| 7×6×5×4×3 |
| 1 |
| 35 |
∴E(X)=1×
| 3 |
| 7 |
| 2 |
| 7 |
| 6 |
| 35 |
| 3 |
| 35 |
| 1 |
| 35 |
点评:本题考查概率的公式与分布列的计算,注意概率计算是基础,平时要加强概率的计算的训练.

练习册系列答案
相关题目
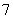 个且形状完全相同,从中任取
个且形状完全相同,从中任取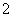 个玩具都是“圆圆”的概率为
个玩具都是“圆圆”的概率为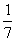 ,
,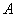 、
、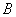 两人不放回从袋中轮流摸取一个玩具,
两人不放回从袋中轮流摸取一个玩具,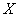 表示游戏终止时取玩具的次数.
表示游戏终止时取玩具的次数.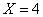 时的概率;
时的概率; ,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,…直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用X表示游戏终止时取玩具的次数.
,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,…直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用X表示游戏终止时取玩具的次数.