题目内容
设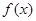 为定义在R上的奇函数,当
为定义在R上的奇函数,当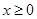 时,
时,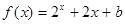 (b为常数),
(b为常数),
则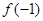 等于( )
等于( )
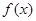 为定义在R上的奇函数,当
为定义在R上的奇函数,当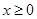 时,
时,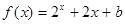 (b为常数),
(b为常数),则
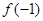 等于( )
等于( )| A.3 | B.-1 | C.1 | D.-3 |
D
分析:由f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),知f(0)=1+b=0,解得b=-1所以当x<0时,f(x)=-2-x+2x+1,由此能求出f(-1).
解:∵f(x)是定义在R上的奇函数,
当x≥0时,f(x)=2x+2x+b(b为常数),
∴f(0)=1+b=0,
解得b=-1
∴f(x)=2x+2x-1.
当x<0时,-f(x)=2-x+2(-x)-1,
∴f(x)=-2-x+2x+1,
∴f(-1)=-2-2+1=-3.
故答案为:-3.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 )·3a的结果是( )
)·3a的结果是( ) C12a
C12a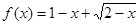 的值域为( )
的值域为( )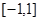
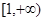

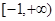
 实数
实数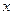 、
、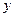 同时满足条件:
同时满足条件: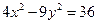 ,且
,且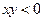 ,
,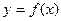 的解析式和定义域;
的解析式和定义域;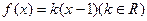 恰有两个不同的实数根,求
恰有两个不同的实数根,求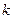 的取值范围
的取值范围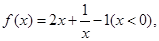 则
则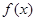 ( )
( )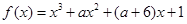 有极大值和极小值,则实数
有极大值和极小值,则实数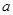 的取值范围是( )
的取值范围是( ) 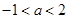
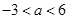
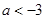 或
或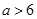
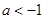 或
或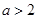
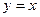 相同的是( )
相同的是( )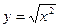
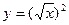
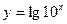
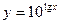
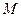 是满足下列性质的函数
是满足下列性质的函数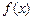 的全体:存在非零常数k, 对定义域中
的全体:存在非零常数k, 对定义域中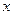 ,等式
,等式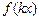 =
=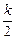 +
+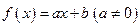 ,
,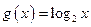 ,则函数
,则函数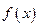 、
、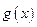 与集合
与集合