题目内容
已知直线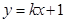 与曲线
与曲线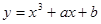 切于点(1, 3),则b的值为()
切于点(1, 3),则b的值为()
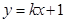 与曲线
与曲线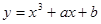 切于点(1, 3),则b的值为()
切于点(1, 3),则b的值为()| A.3 | B.-3 | C.5 | D.-5 |
A
因为(1,3)是直线与曲线的交点,所以把(1,3)代入直线方程即可求出斜率k的值,然后利用求导法则求出曲线方程的导函数,把切点的横坐标x=1代入导函数中得到切线的斜率,让斜率等于k列出关于a的方程,求出方程的解得到a的值,然后把切点坐标和a的值代入曲线方程,即可求出b的值.
解:把(1,3)代入直线y=kx+1中,得到k=2,
求导得:y′=3x2+a,所以y′x=1=3+a=2,解得a=-1,
把(1,3)及a=-1代入曲线方程得:1-1+b=3,
则b的值为3.
故选A
解:把(1,3)代入直线y=kx+1中,得到k=2,
求导得:y′=3x2+a,所以y′x=1=3+a=2,解得a=-1,
把(1,3)及a=-1代入曲线方程得:1-1+b=3,
则b的值为3.
故选A

练习册系列答案
相关题目
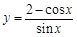 在点
在点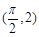 处的切线与直线
处的切线与直线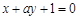 垂直,则
垂直,则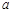 等于
等于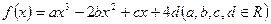 的图象关于原点对称,且
的图象关于原点对称,且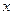 =1时,f(x)取极小值
=1时,f(x)取极小值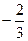 。
。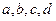 的值;
的值;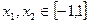 时,求证:
时,求证: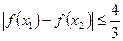 。
。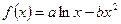 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为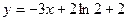 .求
.求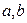 的值;
的值;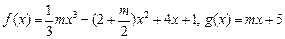 .
. 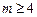 时,求函数
时,求函数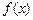 的单调递增区间;
的单调递增区间;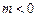 ,使得对任意的
,使得对任意的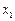 ,
,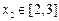 都有
都有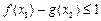 ,若存在,求
,若存在,求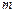 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.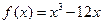 在区间(-∞,-2)与(2,+∞)内是增函数,在(-2,2
在区间(-∞,-2)与(2,+∞)内是增函数,在(-2,2 )内是减函数,那么这个函数的极大值和极小值分别是 。
)内是减函数,那么这个函数的极大值和极小值分别是 。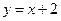 与曲线
与曲线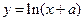 相切,则a=
相切,则a= 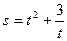 (t是时间,s是位移),则物体在时刻t=2时的速度为____
(t是时间,s是位移),则物体在时刻t=2时的速度为____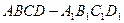 的容积是
的容积是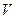 ,里面装有体积为
,里面装有体积为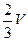 的水,放在水平的地面上(如图所示). 现以顶点
的水,放在水平的地面上(如图所示). 现以顶点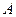 为支撑点,将铁桶倾斜,当铁桶中的水刚好要从顶点
为支撑点,将铁桶倾斜,当铁桶中的水刚好要从顶点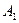 处流出时,棱
处流出时,棱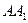 与地面所成角的余弦值为
与地面所成角的余弦值为