题目内容
(本小题满分14分)
已知函数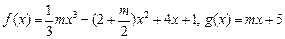 .
.
(1)当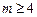 时,求函数
时,求函数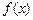 的单调递增区间;
的单调递增区间;
(2)是否存在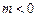 ,使得对任意的
,使得对任意的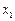 ,
,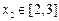 都有
都有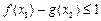 ,若存在,求
,若存在,求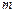 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
已知函数
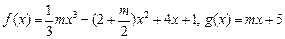 .
. (1)当
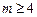 时,求函数
时,求函数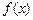 的单调递增区间;
的单调递增区间;(2)是否存在
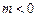 ,使得对任意的
,使得对任意的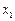 ,
,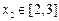 都有
都有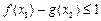 ,若存在,求
,若存在,求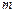 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.解:
 (1)
(1)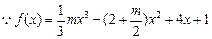
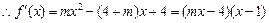 . ………..2分
. ………..2分若
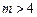 时,则
时,则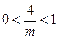 ,
,此时
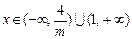 都有
都有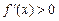 ,[
,[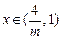 有
有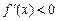 .
.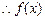 的单调递增区间为
的单调递增区间为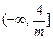 和
和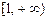 . ………….4分
. ………….4分ii)若
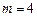 ,则
,则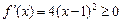 ,
,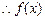 的单调递增区间为
的单调递增区间为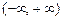 . …………6分
. …………6分(2)当
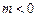 时,
时,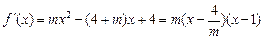 且
且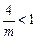 ,
,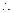 当
当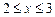 时,都有
时,都有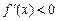 .
. 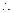 此
此 时,
时,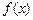 在
在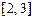 上单调递减
上单调递减  .………..9分
.………..9分又
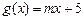 在
在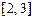 上单调递减.
上单调递减.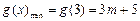 . ………11分
. ………11分 由已知
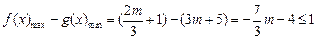
解得
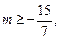 又
又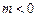 .
.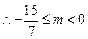 . ………….13分
. ………….13分综上所述,存在
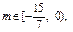 使对任意
使对任意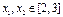
 ,都有
,都有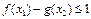 成立…14分
成立…14分略

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
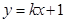 与曲线
与曲线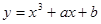 切于点(1, 3),则b的值为()
切于点(1, 3),则b的值为()
 (
( )在
)在 时有极值,其图象在点
时有极值,其图象在点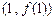 处的切线与直线
处的切线与直线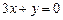 平行。
平行。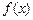 的单调区间。
的单调区间。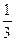
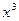 +
+ 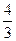 .
.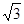
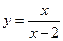 在点
在点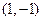 处的切线方程为
处的切线方程为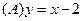
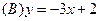
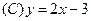
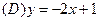
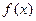 的定义域为开区间
的定义域为开区间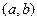 ,导函数
,导函数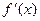 在
在 图
图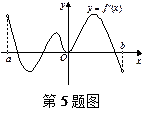

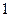 个 B
个 B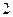 个 C
个 C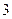 个 D
个 D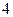
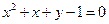 ,则下列
,则下列 各点中在曲线C上的点是( )
各点中在曲线C上的点是( )