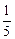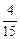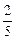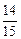题目内容
(10分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上的点数为横坐标x、第二次向上的点数为纵坐标y的点(x, y)在直线
x-y=3的下方区域的概率。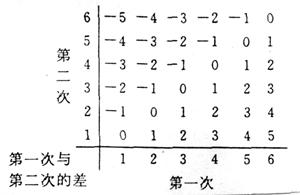
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上的点数为横坐标x、第二次向上的点数为纵坐标y的点(x, y)在直线
x-y=3的下方区域的概率。

(1)两数之和为6的概率为
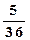
(2)
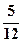
(3)
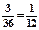
解:(1)两数之和为6的概率为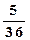 。
。
(2)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由下面的列表可知,事件A中含有其中的15个等可能基本事件,所以P(A)=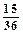 =
= ,
,
所以两数之积是6的倍数的概率为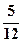 。
。
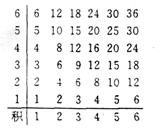
(3)此问题中含有36个等可能基本事件,点(x,y)在直线x-y="3的下方区域含有其中3个基本等可能基本事件,所以点(x," y)在直线x-y=3的上方区域的概率为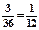 。
。
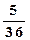 。
。(2)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由下面的列表可知,事件A中含有其中的15个等可能基本事件,所以P(A)=
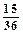 =
= ,
,所以两数之积是6的倍数的概率为
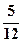 。
。
(3)此问题中含有36个等可能基本事件,点(x,y)在直线x-y="3的下方区域含有其中3个基本等可能基本事件,所以点(x," y)在直线x-y=3的上方区域的概率为
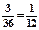 。
。
练习册系列答案
相关题目
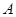 发生的概率为
发生的概率为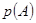 ,则
,则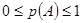
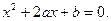 (1)若
(1)若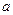 是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若
是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若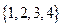 ,
,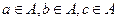 ,则以
,则以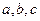 为三边构成三角形的概率为
为三边构成三角形的概率为
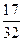

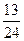



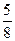

 个电子元件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将2个次品全部找出的概率( )
个电子元件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将2个次品全部找出的概率( )