题目内容
设奇函数f(x)的定义域为(﹣∞,0)∪(0+∞),且在(0,+∞)上为增函数.
(1)若f(1)=0,解关于x的不等式:f(1+logax)>0(0<a<1).
(2)若f(﹣2)=﹣1,当m>0,n>0时,恒有f(m n)=f(m)+f(n),求|f(t)+1|<1时,t的取值范围.
n)=f(m)+f(n),求|f(t)+1|<1时,t的取值范围.
(1)若f(1)=0,解关于x的不等式:f(1+logax)>0(0<a<1).
(2)若f(﹣2)=﹣1,当m>0,n>0时,恒有f(m
 n)=f(m)+f(n),求|f(t)+1|<1时,t的取值范围.
n)=f(m)+f(n),求|f(t)+1|<1时,t的取值范围. 解:(1)∵奇函数f(x)在(0,+∞)上为增函数,则在(﹣∞,0)也单调递增
∵f(1)=﹣f(﹣1)=0
∴f(﹣1)=0
当x>1或﹣1<x<0时,f(x)>0;
当0<x<1或x<﹣1时,f(x)<0
∵f(1+logax)>0
∴1+logax>1或﹣1<1+logax<0
∵0<a<1
∴0<x<1或a﹣1<x<2﹣2
(2)∵f(﹣2)=﹣1
∴f(2)=﹣f(﹣2)=1
∵m>0,n>0时,恒有f(m n)=f(m)+f(n),
n)=f(m)+f(n),
∴f(4)=2f(2)=2,f(﹣4)=﹣2,f(1)=2f(1),
则f(1)=﹣f(﹣1)=0
∵|f(t)+1|<1
∴﹣2<f(t)<0
∴﹣4<t<﹣1
∵f(1)=﹣f(﹣1)=0
∴f(﹣1)=0
当x>1或﹣1<x<0时,f(x)>0;
当0<x<1或x<﹣1时,f(x)<0
∵f(1+logax)>0
∴1+logax>1或﹣1<1+logax<0
∵0<a<1
∴0<x<1或a﹣1<x<2﹣2
(2)∵f(﹣2)=﹣1
∴f(2)=﹣f(﹣2)=1
∵m>0,n>0时,恒有f(m
 n)=f(m)+f(n),
n)=f(m)+f(n), ∴f(4)=2f(2)=2,f(﹣4)=﹣2,f(1)=2f(1),
则f(1)=﹣f(﹣1)=0
∵|f(t)+1|<1
∴﹣2<f(t)<0
∴﹣4<t<﹣1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
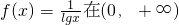 是减函数;
是减函数;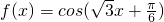 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;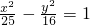 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;