题目内容
定义在 上的函数
上的函数 满足下列两个条件:⑴对任意的
满足下列两个条件:⑴对任意的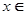
 恒有
恒有 成立;⑵当
成立;⑵当 时,
时, ;如果关于
;如果关于 的方程
的方程 恰有两个不同的解,那么实数
恰有两个不同的解,那么实数 的取值范围是 .
的取值范围是 .
 上的函数
上的函数 满足下列两个条件:⑴对任意的
满足下列两个条件:⑴对任意的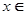
 恒有
恒有 成立;⑵当
成立;⑵当 时,
时, ;如果关于
;如果关于 的方程
的方程 恰有两个不同的解,那么实数
恰有两个不同的解,那么实数 的取值范围是 .
的取值范围是 .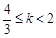
依题意可得当 时,
时, ,则
,则 。因为方程
。因为方程 恰有两个不同的解,所以函数
恰有两个不同的解,所以函数 与过定点
与过定点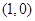 且斜率存在的直线在
且斜率存在的直线在 上恰有两个不同交点。根据函数图象可得,当直线
上恰有两个不同交点。根据函数图象可得,当直线 经过点
经过点 时,直线与
时,直线与 恰有1个交点,此时
恰有1个交点,此时 。当
。当 时直线开始与
时直线开始与 有两个不同交点。当直线
有两个不同交点。当直线 经过点
经过点 时,直线与
时,直线与 恰有2个交点,此时
恰有2个交点,此时 。当
。当 时直线开始与
时直线开始与 有三个不同交点。综上可得
有三个不同交点。综上可得

 时,
时, ,则
,则 。因为方程
。因为方程 恰有两个不同的解,所以函数
恰有两个不同的解,所以函数 与过定点
与过定点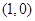 且斜率存在的直线在
且斜率存在的直线在 上恰有两个不同交点。根据函数图象可得,当直线
上恰有两个不同交点。根据函数图象可得,当直线 经过点
经过点 时,直线与
时,直线与 恰有1个交点,此时
恰有1个交点,此时 。当
。当 时直线开始与
时直线开始与 有两个不同交点。当直线
有两个不同交点。当直线 经过点
经过点 时,直线与
时,直线与 恰有2个交点,此时
恰有2个交点,此时 。当
。当 时直线开始与
时直线开始与 有三个不同交点。综上可得
有三个不同交点。综上可得


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,
,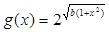 ,
, ,且
,且 ,
, .
. 、
、 的解析式;
的解析式;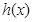 为定义在
为定义在 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数 恒成立;②当
恒成立;②当 时
时 .
. 时,函数
时,函数 在区间
在区间 上的解的个数.
上的解的个数. ,
, ,其中
,其中 R.
R. 的单调性;
的单调性;
 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数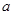 的取值范围;
的取值范围;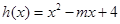 ,当
,当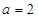 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围。
的取值范围。 、
、 两点满足条件:①点
两点满足条件:①点 图像上;②点
图像上;②点
 ,则
,则 ,
, ,记
,记 .
. ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;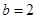 ,且
,且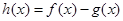 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围; ,设函数
,设函数 的图象
的图象 与函数
与函数 图象
图象 交于点
交于点 、
、 ,过线段
,过线段 的中点作
的中点作 轴的垂线分别交
轴的垂线分别交 、
、 ,请判断
,请判断 切线能否平行,并说明你的理由.
切线能否平行,并说明你的理由. ,则
,则 = .
= . ,方程
,方程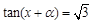 的一个解为
的一个解为 ,则
,则 等于 .
等于 .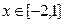 时,函数
时,函数 的值域是___________
的值域是___________