题目内容
 如图,空间四边形OABC中,
如图,空间四边形OABC中,| OA |
| OB |
| OC |
| 1 |
| 2 |
| MN |
分析:由题意,把
,
,
三个向量看作是基向量,由图形根据向量的线性运算,将
用三个基向量表示出来,即可得到答案,选出正确选项
| OA |
| OB |
| OC |
| MN |
解答:解:由题意
=
+
+
=
+
-
+
=-
+
+
-
=-
+
+
又
=
,
=
,
=
∴
=-
+
+
故选A
| MN |
| MA |
| AB |
| BN |
| 2 |
| 3 |
| OA |
| OB |
| OA |
| 1 |
| 2 |
| BC |
| 1 |
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OC |
| 1 |
| 2 |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
又
| OA |
| a |
| OB |
| b |
| OC |
| c |
∴
| MN |
| 1 |
| 3 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
故选A
点评:本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,空间四边形OABC中,
如图,空间四边形OABC中, 已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,
已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,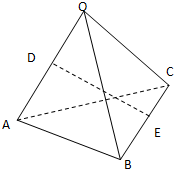 如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE
如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE 