题目内容
在平面直角坐标系中,已知直线l:y=-1,定点F(0,1),过平面内动点P作PQ丄l于Q点,且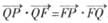 •
•
(I )求动点P的轨迹E的方程;
(II)过点P作圆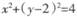 的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
【答案】
(Ⅰ)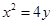 . (Ⅱ)
. (Ⅱ)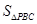 的最小值为32.
的最小值为32.
【解析】(Ⅰ)设出点的坐标,根据条件列式化简即可;(Ⅱ)先求出切线方程,然后利用弦长公式求出三角形的底边,然后利用点到直线的距离求出高,进一步求出面积的最值
(Ⅰ)设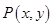 ,则
,则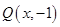 ,∵
,∵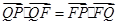 ,
,
∴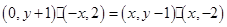 .
…………………2分
.
…………………2分
即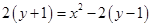 ,即
,即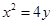 ,
,
所以动点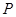 的轨迹
的轨迹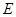 的方程
的方程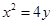 .
…………………………4分
.
…………………………4分
(Ⅱ)解法一:设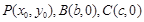 ,不妨设
,不妨设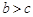 .
.
直线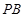 的方程:
的方程: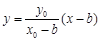 ,化简得
,化简得 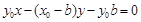 .
.
又圆心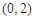 到
到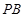 的距离为2,
的距离为2,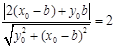 ,
,
故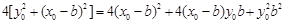 ,易知
,易知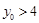 ,上式化简得
,上式化简得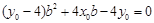 ,
同理有
,
同理有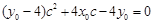 . …………6分
. …………6分
所以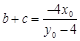 ,
,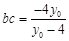 ,…………………8分
,…………………8分
则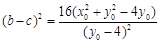 .
.
因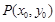 是抛物线上的点,有
是抛物线上的点,有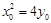 ,
,
则 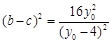 ,
,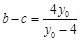 .
………………10分
.
………………10分
所以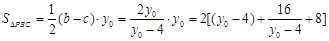
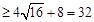 .
.
当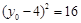 时,上式取等号,此时
时,上式取等号,此时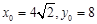 .
.
因此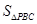 的最小值为32.
……………………12分
的最小值为32.
……………………12分
解法二:设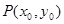 , 则
, 则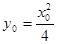 ,
,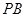 、
、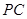 的斜率分别为
的斜率分别为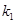 、
、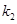 ,
,
则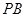 :
: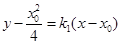 ,令
,令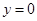 得
得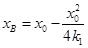 ,同理得
,同理得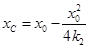 ;
;
所以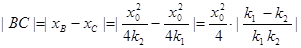 ,……………6分
,……………6分
下面求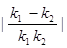 ,由
,由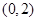 到
到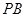 :
: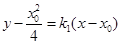 的距离为2,得
的距离为2,得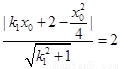 ,
,
因为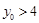 ,所以
,所以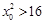 ,化简得
,化简得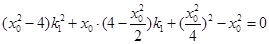 ,
,
同理得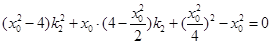 …………………8分
…………………8分
所以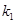 、
、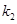 是
是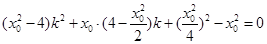 的两个根.
的两个根.
所以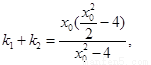

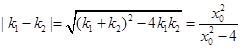 ,
,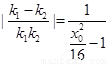 ,
,
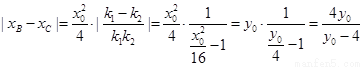 ,……………10分
,……………10分
所以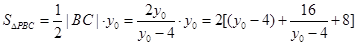
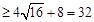 .
.
当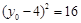 时,上式取等号,此时
时,上式取等号,此时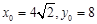 .
.
因此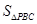 的最小值为32.
的最小值为32.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目