题目内容

当x、y满足不等式组
2≤x≤4
y≥3
x+y≤8
时，目标函数k=3x-2y的最大值为
 
．
分析：作出可行域，将目标函数变形，作出直线y=
3
2
x，将直线平移至（4，3）时，纵截距最小，k最大，将（4，3）代入k求出其最大值．
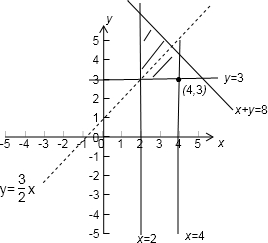解答：精英家教网解：作出可行域将目标函数k=3x-2y变形为y=
3
2
x-
k
2

作出直线y=
3
2
x，将其平移至（4，3）时纵截距最小，k最大
所以k的最大值为3×4-2×3=6
故答案为：6
点评：本题考查画不等式组表示的平面区域，利用可行域求出目标函数的最值．
练习册系列答案
相关题目
当x、y满足不等式组
y≤x
y≥-1
x+y≤1
时，目标函数t=2x+y的最小值是
 
．
当x，y满足不等式组
x+y≥4
x+4≥y
x≤4
时，点（4，8）为目标函数z=ax+2y（a＜0）取得最大值时的唯一最优解，则实数a的取值范围是
（-2，0）
（-2，0）
．
当x、y满足不等式组
0≤x≤2
y≥0
y≤x+1
时，目标函数t=x+y的最大值是
5
5
．
（2004•虹口区一模）当x，y满足不等式组
1≤x≤5
y≥2
x+y≤10
时，目标函数K=x-y的最小值是
-8
-8
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网