题目内容
过直线y=2上一点P向单位圆作两切线,切点分别为A、B.(I)若A、B两点所在直线与直线y=-2交于点M,若点M的横坐标的取值范围为[1,
| 5 | 2 |
(II)在(I)的条件下,是否存在一条切线作为入射线射到直线y=-2上,其反射线也与单位圆相切?若存在,求出该切线方程;若不存在,请说明理由.
分析:(I)求出以P为圆心,以AP为半径的圆的方程,利用圆系方程,求出公共弦AB的方程,将M点的坐标代入AB的方程,利用点M的横坐标的取值范围为[1,
]可以求得P点横坐标的取值范围;
(Ⅱ)设存在一条切线作为入射线射到直线y=-2上,其反射线也与单位圆相切,满足要求的法线为y轴,求得入射线的方程后,验证即可.
| 5 |
| 2 |
(Ⅱ)设存在一条切线作为入射线射到直线y=-2上,其反射线也与单位圆相切,满足要求的法线为y轴,求得入射线的方程后,验证即可.
解答:解:(I)设P(x0,2)由题意可得PA2=OP2-OA2=(x02+4)-1,
所以以P为圆心,以AP为半径的圆的方程为(x-x0)2+(y-2)2=x02+3,…①
又单位圆的方程为x2+y2=1…②
直线AB的方程就是两个圆的公共弦的方程,
所以①-②得x0x+2y=1,由
得M(
,-2),
又点M的横坐标的取值范围为[1,
],由 1≤
≤
得2≤x0≤5;
(Ⅱ)设存在一条切线作为入射线射到直线y=-2上,入射点为P,其反射线也与单位圆相切,
由题意可知法线必为y轴,
所以点P坐标为(-2,0),设入射线与单位圆相切于点N,在直角三角形PNO中,sin∠OPN=
,∠OPN=30°
所以入射光线AP的倾斜角为60°,kAP=tan 60° =
,直线AP又经过点(-2,0)
所以入射线AP的方程为:y=
x-2;由
得x=
∈[2,5];
所以存在这样的入射光线满足题意,其方程为:y=
x-2.
所以以P为圆心,以AP为半径的圆的方程为(x-x0)2+(y-2)2=x02+3,…①
又单位圆的方程为x2+y2=1…②
直线AB的方程就是两个圆的公共弦的方程,
所以①-②得x0x+2y=1,由
|
| 5 |
| x0 |
又点M的横坐标的取值范围为[1,
| 5 |
| 2 |
| 5 |
| x0 |
| 5 |
| 2 |
(Ⅱ)设存在一条切线作为入射线射到直线y=-2上,入射点为P,其反射线也与单位圆相切,
由题意可知法线必为y轴,
所以点P坐标为(-2,0),设入射线与单位圆相切于点N,在直角三角形PNO中,sin∠OPN=
| 1 |
| 2 |
所以入射光线AP的倾斜角为60°,kAP=tan 60° =
| 3 |
所以入射线AP的方程为:y=
| 3 |
|
| 4 |
| 3 |
| 3 |
所以存在这样的入射光线满足题意,其方程为:y=
| 3 |
点评:本题考查直线的一般式方程,圆的切线方程,圆系方程,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
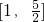 ,求P点横坐标的取值范围;
,求P点横坐标的取值范围; ,求P点横坐标的取值范围;
,求P点横坐标的取值范围;