Question

（2010•衢州一模）过直线y=x上一点P作圆C：（x-5）²+（y-1）²=2的两条切线l₁，l₂，切点分别为A，B，则四边形PABC面积的最小值为（　　）

• A．2
• B．

  3

• C．2

  3

• D．4

Answer 1

分析：过圆心C作直线y=x的垂线，垂直为P时，做出两条切线，此时四边形PABC面积最小，求出即可．

解答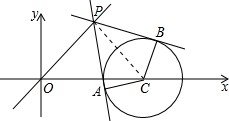：解：如图所示，CP⊥OP，PA，PB分别为圆C的切线，此时四边形PACB面积最小，
∵圆心（5，1）到直线y=x的距离d=|PC|=

4

2

=2

2

，r=|AC|=

2

，
∴|PA|=

(2 2 )2-( 2 )2

=

6

，
则S_{四边形PACB}=2S_△PAC=2×

1

2

×

6

×

2

=2

3

．
故选C

点评：此题考查了直线与圆的位置关系，直线与圆的位置关系由圆心到直线的距离d与半径r比较大小来判定．