题目内容
（1）求
的值；
（2）若α＞0，β＞0，且α+β=15°，求
的值．
| ||
|
（2）若α＞0，β＞0，且α+β=15°，求
| sinα+cos15°sinβ |
| cosα-sin15°sinβ |
分析：（1）原式化简成平方和，即可求解
（2）原式利用两角和与差的正弦函数公式化简，再利用特殊角的三角函数值计算即可求出值．
（2）原式利用两角和与差的正弦函数公式化简，再利用特殊角的三角函数值计算即可求出值．
解答：解：
（1）原式=
=
=-1…5分
（2）∵α＞0，β＞0，且α+β=15°，∴α=15°-β…9分
∴原式=
=
=tan15°=tan（45°-30°）=
=2-
…12分
（1）原式=
| ||
|
| cos10°-sin10° |
| sin10°-cos10° |
（2）∵α＞0，β＞0，且α+β=15°，∴α=15°-β…9分
∴原式=
| sin(15°-β)+cos15°cosβ |
| cos(15°-β)-sin15°sinβ |
| 2sin15°cosβ |
| 2cos15°cosβ |
| tan45°-tan30° |
| 1+tan45°tan30° |
| 3 |
点评：此题考查了两角和与差的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
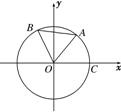如图，点A，B是单位圆上的两点，A，B点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为（