题目内容
等差数列{an}中,a1=1,前n项和为Sn,等比数列{bn}各项均为正数,b1=2,且S2+b2=7,S4-b3=2.
(1)求an与bn;
(2)设![]() ,Tn=c1·c2·c3…cn求证:
,Tn=c1·c2·c3…cn求证:![]() (n∈N+).
(n∈N+).
答案:
解析:
解析:
|
解:(1)设等差数列 由题知: 解直得,q=2或q=-8(舍去),d=1; 5分 (2)证明: 法一、 下面用数学归纳法证明 (1) (2) 则当 = 综上所述原命题成立. 14分 法二、 法三、设数列 |

练习册系列答案
相关题目
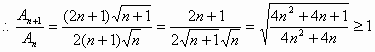 12分
12分