题目内容
已知正数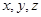 满足
满足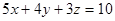 ,
,
(1) 求证: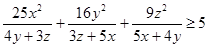 ; (2) 求
; (2) 求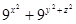 的最小值.
的最小值.
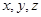 满足
满足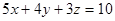 ,
,(1) 求证:
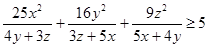 ; (2) 求
; (2) 求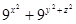 的最小值.
的最小值.(1) 解: 根据柯西不等式,得
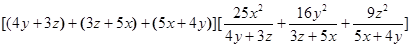
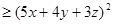 ,
,
因为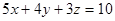 ,所以
,所以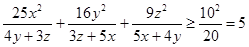 .
.
(2) 解: 根据均值不等式, 得 ,
,
当且仅当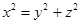 时, 等号成立.根据柯西不等式, 得
时, 等号成立.根据柯西不等式, 得
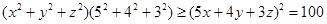 , 即
, 即 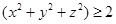 ,
,
当且仅当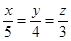 时, 等号成立.综上,
时, 等号成立.综上, 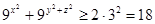 .当且仅当
.当且仅当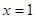 ,
,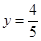 ,
,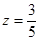 时, 等号成立,所以
时, 等号成立,所以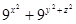 的最小值为18
的最小值为18
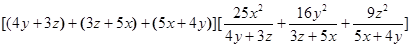
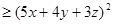 ,
,因为
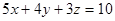 ,所以
,所以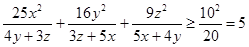 .
. (2) 解: 根据均值不等式, 得
 ,
,当且仅当
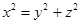 时, 等号成立.根据柯西不等式, 得
时, 等号成立.根据柯西不等式, 得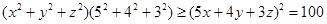 , 即
, 即 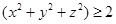 ,
,当且仅当
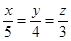 时, 等号成立.综上,
时, 等号成立.综上, 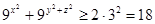 .当且仅当
.当且仅当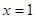 ,
,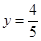 ,
,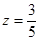 时, 等号成立,所以
时, 等号成立,所以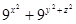 的最小值为18
的最小值为18略

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 ,求证:
,求证: .
.
 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。 在
在 上恒成立,求实数
上恒成立,求实数 的最大值。
的最大值。 ,则
,则 的最大值为 ▲ ;
的最大值为 ▲ ;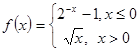 ,若
,若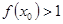 ,则
,则 的取值范围( )
的取值范围( )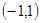
 [
[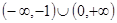
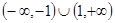
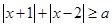 对任意
对任意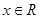 恒成立,则
恒成立,则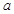 的取值范围是
的取值范围是 .
.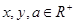 ,且
,且 恒成立,则
恒成立,则 的最小值是( )。
的最小值是( )。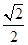



 ,
, ,
, ,则( )
,则( )


