题目内容
7.给出下列四个命题:①点(1,-2,4)关于原点对称的对称点的坐标为(-1,2,-4);
②若一个圆柱的侧面展开图是一个长和宽分别为6和4的矩形,则这个圆柱的体积为$\frac{24}{π}$;
③经过点(1,1)且在两坐标轴上的截距相等的直线是x+y=2;
④把一个三棱柱的各个面伸展成平面,则可把空间分为21部分.
其中正确的命题有①④.
分析 ①利用关于原点对称的对称点的坐标的特点即可得出;
②若一个圆柱的侧面展开图是一个长和宽分别为6和4的矩形,则2πr=6,解得$r=\frac{3}{π}$,利用圆柱的体积计算公式即可得出;
③分截距为0与不等于0讨论,即可判断出正误;
④把一个三棱柱的各个面伸展成平面,查一下即可得出.
解答 解:①点(1,-2,4)关于原点对称的对称点的坐标为(-1,2,-4),正确;
②若一个圆柱的侧面展开图是一个长和宽分别为6和4的矩形,则2πr=6,解得$r=\frac{3}{π}$,∴这个圆柱的体积V=$π(\frac{3}{π})^{2}×4$=$\frac{36}{π}$,因此不正确;
③经过点(1,1)且在两坐标轴上的截距相等的直线是x+y=2或y=x,因此不正确;
④把一个三棱柱的各个面伸展成平面,则可把空间分为21部分,正确.
故正确答案为:①④.
点评 本题查克拉简易逻辑的判定方法、关于原点对称的对称点的坐标的特点、圆柱的展开图、直线的截距式、三棱柱,考查了分类讨论与空间想象能力及其推理能力,属于中档题.

练习册系列答案
相关题目
7.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为45°,且$\overrightarrow{a}$=(2,-2),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
12.已知{an}是等差数列,{bn}是正项等比数列,若a11=b10,则( )
| A. | a13+a9=b14b6 | B. | a13+a9=b14+b6 | C. | a13+a9≥b14+b6 | D. | a13+a9≤b14+b6 |
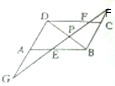 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.