题目内容
【题目】已知圆心在直线x+y﹣1=0上且过点A(2,2)的圆C1与直线3x﹣4y+5=0相切,其半径小于5.
(1)若C2圆与圆C1关于直线x﹣y=0对称,求圆C2的方程;
(2)过直线y=2x﹣6上一点P作圆C2的切线PC,PD,切点为C,D,当四边形PCC2D面积最小时,求直线CD的方程.
【答案】
(1)解:由题意,设C1(a,1﹣a),则
∵过点A(2,2)的圆C1与直线3x﹣4y+5=0相切,
∴ ![]() =
= ![]() ,
,
∴(a﹣2)(a﹣62)=0
∵半径小于5,
∴a=2,此时圆C1的方程为(x﹣2)2+(y+1)2=9,
∵C2圆与圆C1关于直线x﹣y=0对称,
∴圆C2的方程为(x+1)2+(y﹣2)2=9;
(2)解:设P(a,2a﹣6),圆C2的半径r=2,
∴四边形PCC2D面积S=2 ![]() =
= ![]() =3|PD|,
=3|PD|,
|PD|= ![]() =
= ![]() ,
,
∴a=3时,|PD|min= ![]() ,此时面积最小为3
,此时面积最小为3 ![]() ,P(3,0).
,P(3,0).
∵C,D在以PC2为直径的圆上,
∴方程为(x﹣1)2+(y﹣1)2=5,
∵圆C2的方程为(x+1)2+(y﹣2)2=9,
∴两个方程相减,可得CD的方程为4x﹣2y﹣1=0.
【解析】(1)利用过点A(2,2)的圆C1与直线3x﹣4y+5=0相切, ![]() =
= ![]() ,求出圆心与半径,可得圆C1的方程,利用C2圆与圆C1关于直线x﹣y=0对称,即可求圆C2的方程;(2)求出四边形PCC2D面积最小值,可得以PC2为直径的圆的方程,即可求直线CD的方程.
,求出圆心与半径,可得圆C1的方程,利用C2圆与圆C1关于直线x﹣y=0对称,即可求圆C2的方程;(2)求出四边形PCC2D面积最小值,可得以PC2为直径的圆的方程,即可求直线CD的方程.
【考点精析】掌握直线与圆的三种位置关系是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

 53天天练系列答案
53天天练系列答案【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 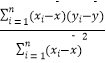 )=
)= 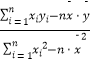 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?