题目内容
设m，n，a，b∈R，若m2+n2=1，a2+b2=4，那么am+bn有（ ）
分析：利用三角代换及两角差的余弦公式，把am+bn 化为2cos（θ-β），再利用余弦函数的有界性，求出am+bn的最大值．
解答：解：三角代换：令m=cosθ，n=sinθ，a=2cosβ，b=2sinβ．
∴am+bn=2cosθcosβ+2sinθsinβ=2cos（θ-β）≤2，
故am+bn的最大值是2，
故选C．
∴am+bn=2cosθcosβ+2sinθsinβ=2cos（θ-β）≤2，
故am+bn的最大值是2，
故选C．
点评：本题主要考查了把普通方程化为参数方程的方法，两角差的余弦公式的应用，属于基础题．
练习册系列答案
相关题目
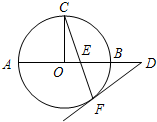A（选修4-1：几何证明选讲）
),f(
),f(
),f(
)的大小顺序依次是__________.
