题目内容
设实数a,b,x,y满足a2+b2=1,x2+y2=3,则ax+by的取值范围为
[-
,
]
| 3 |
| 3 |
[-
,
]
.| 3 |
| 3 |
分析:先根据条件令a=cosα,b=sinα,x=
cosβ,y=
sinβ,α、β∈R,然后代入ax+by,利用余弦函数的两角差公式进行化简,最后根据余弦函数的有界性可求出所求.
| 3 |
| 3 |
解答:解:∵a2+b2=1,x2+y2=3
∴设a=cosα,b=sinα,x=
cosβ,y=
sinβ,α、β∈R
∴ax+by=
cosαcosβ+
sinαsinβ
=
(cosαcosβ+sinαsinβ)
=
cos(α-β)
∵-1≤cos(α-β)≤1
∴-
≤
cos(α-β)≤
即ax+by的取值范围为[-
,
]
故答案为:[-
,
]
∴设a=cosα,b=sinα,x=
| 3 |
| 3 |
∴ax+by=
| 3 |
| 3 |
=
| 3 |
=
| 3 |
∵-1≤cos(α-β)≤1
∴-
| 3 |
| 3 |
| 3 |
即ax+by的取值范围为[-
| 3 |
| 3 |
故答案为:[-
| 3 |
| 3 |
点评:本题主要考查了圆的参数方程,以及余弦函数的两角和与差,同时考查了三角函数的有界性,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
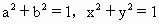 ,则ax+by≤________.
,则ax+by≤________.