题目内容
某学校要对学生进行身体素质全面测试,对每位学生都要进行9选3考核(即共9项测试,随机选取3项),若全部合格,则颁发合格证;若不合格,则重新参加下期的9选3考核,直至合格为止,若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为
,第二次参加考试合格的概率为
,第三次参加考试合格的概率为
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
(1)求小李第一次考试即通过的概率P;
(2)求小李参加考核的次数ξ分布列.
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 5 |
(1)求小李第一次考试即通过的概率P;
(2)求小李参加考核的次数ξ分布列.
分析:(1)若小李选中的士项中无“引体向上”一次通过的概率为
,若选的三项中含引体向上,一次通过的概率为
×
,由此能求出小李第一次考试即通过的概率P.
(2)由题设知ξ可取1,2,3,4,分别求出其概率,能够求出ξ的分布列.
| ||
|
| ||
|
| 1 |
| 2 |
(2)由题设知ξ可取1,2,3,4,分别求出其概率,能够求出ξ的分布列.
解答:解:(1)若小李选中的士项中无“引体向上”一次通过的概率为
,
若选的三项中含引体向上,一次通过的概率为
×
,
∴小李第一次考试即通过的概率P=
+
×
=
.
(2)由题设条件知ξ可取1,2,3,4,
P(ξ=1)=
,
P(ξ=2)=
×(
+
×
)=
,
P(ξ=3)=
×
×
×(
+
×
)=
,
P(ξ=4)=
×
×
×
×
=
∴ξ的分布列为:
| ||
|
若选的三项中含引体向上,一次通过的概率为
| ||
|
| 1 |
| 2 |
∴小李第一次考试即通过的概率P=
| C83 |
| C93 |
| C82 |
| C93 |
| 1 |
| 2 |
| 5 |
| 6 |
(2)由题设条件知ξ可取1,2,3,4,
P(ξ=1)=
| 5 |
| 6 |
P(ξ=2)=
| 1 |
| 6 |
| C83 |
| C93 |
| C82 |
| C93 |
| 2 |
| 3 |
| 4 |
| 27 |
P(ξ=3)=
| 1 |
| 6 |
| C82 |
| C93 |
| 1 |
| 3 |
| C83 |
| C93 |
| C82 |
| C93 |
| 4 |
| 5 |
| 7 |
| 405 |
P(ξ=4)=
| 1 |
| 6 |
| C82 |
| C93 |
| 1 |
| 3 |
| C82 |
| C93 |
| 1 |
| 5 |
| 1 |
| 810 |
∴ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
点评:本题考查离散型随机变量的分布列和数学期望,是中档题,在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意排列组合和概率知识的灵活运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
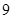 选
选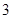 考核(即共
考核(即共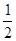 ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为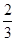 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为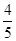 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.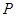 ;
;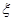 分布列.
分布列.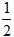 ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为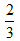 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为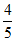 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过. ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过. ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.