题目内容
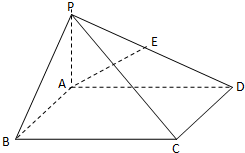 已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2.
已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2.(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)若E是PD的中点,求异面直线AE与PC所成角的余弦值;
(Ⅲ)在BC边上是否存在一点G,使得D点到平面PAG的距离为1?若存在,求出BG的值;若不存在,请说明理由.
分析:法一:(Ⅰ)要证平面PDC⊥平面PAD,只需证明平面PDC的中心CD,垂直平面PAD内的两条相交直线PA、AD即可;
(Ⅱ)CD的中点为F,连接EF、AF,说明∠AEF是异面直线AE与PC所成角或其补角,解三角形求异面直线AE与PC所成角的余弦值;
(Ⅲ)在BC边上存在一点G,设BG=x,过点D作DM⊥AG于M.利用S△AGD=
AG•DM,推出线段DM的长是点D到平面PAG的距离为1.
法二:建立空间直角坐标系,推出
•
=0 ,
•
=0证明CD⊥平面PAD,然后证明 平面PDC⊥平面PAD;利用cos<
,
>=
求解(Ⅱ).则G(1,x,0).利用2S△ADG=S矩形ABCD,求出x的值,即可确定存在一点G.
(Ⅱ)CD的中点为F,连接EF、AF,说明∠AEF是异面直线AE与PC所成角或其补角,解三角形求异面直线AE与PC所成角的余弦值;
(Ⅲ)在BC边上存在一点G,设BG=x,过点D作DM⊥AG于M.利用S△AGD=
| 1 |
| 2 |
法二:建立空间直角坐标系,推出
| CD |
| AD |
| CD |
| AP |
| AE |
| PC |
| ||||
|
|
解答: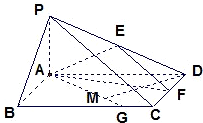 法一:(Ⅰ)证明:∵PA⊥平面ABCD,
法一:(Ⅰ)证明:∵PA⊥平面ABCD,
∴PA⊥CD.(1分)
∵四边形ABCD是矩形,
∴AD⊥CD.
又PA∩AD=A
∴CD⊥平面PAD.(3分)
又∵CD?平面PDC,
∴平面PDC⊥平面PAD.(5分)
(Ⅱ)解:设CD的中点为F,连接EF、AF.
∵E是PD中点,
∴EF∥PC.
∴∠AEF是异面直线AE与PC所成角或其补角.(7分)
由PA=AB=1,BC=2,计算得AE=
PD=
,EF=
PC=
,AF=
,cos∠AEF=
=
=-
,(9分)
∴异面直线AE与PC所成角的余弦值为
.(10分)
(Ⅲ)解:假设在BC边上存在点G,使得点D到平面PAG的距离为1.
设BG=x,过点D作DM⊥AG于M.
∵PA⊥平面ABCD,
∴PA⊥DM,PA∩AG=A.
∴DM⊥平面PAG.
∴线段DM的长是点D到平面PAG的距离,即DM=1.(12分)
又S△AGD=
AG•DM=
=1,
解得x=
<2.
所以,存在点G且当BG=
时,使得点D到平面PAG的距离为1.(14分)
法二:以A为原点,AB所在直线为x轴,AD所在直线为y轴,
AP所在直线为z轴建立空间直角坐标系,则A(0,0,0),
B(1,0,0),C(1,2,0),
D(0,2,0),E(0,1,),
P(0,0,1).
∴
=(-1,0,0),
=(0,2,0),
=(0,0,1),
=(0,1,),
=(1,2,-1).(2分)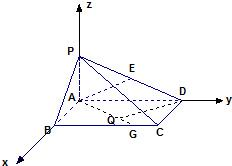
(Ⅰ)∵
•
=0,
∴CD⊥AD.
∵
•
=0,
∴CD⊥AP.
又AP∩AD=A,
∴CD⊥平面PAD.(5分)
∵CD?平面PAD,
∴平面PDC⊥平面PAD.(7分)
(Ⅱ)∵cos<
,
>=
=
=
,(9分)
∴异面直线AE与PC所成角的余弦值为
.(10分)
(Ⅲ)假设BC边上存在一点G满足题设条件,令BG=x,则G(1,x,0).
作DQ⊥AG于Q,
∵PA⊥平面ABCD,
∴PA⊥DQ.
又PA∩AG=A,
∴DQ⊥面PAG.
∴线段DQ的长是点D到平面PAG的距离,即DQ=1.(12分)
∵2S△ADG=S矩形ABCD,
∴|
|•|
|=|
|•|
|=2.
∴|
|=2.
又AG=
,
∴x=
<2.
故存在点G,当BG=
时,使点D到平面PAG的距离为1.(14分)
 法一:(Ⅰ)证明:∵PA⊥平面ABCD,
法一:(Ⅰ)证明:∵PA⊥平面ABCD,∴PA⊥CD.(1分)
∵四边形ABCD是矩形,
∴AD⊥CD.
又PA∩AD=A
∴CD⊥平面PAD.(3分)
又∵CD?平面PDC,
∴平面PDC⊥平面PAD.(5分)
(Ⅱ)解:设CD的中点为F,连接EF、AF.
∵E是PD中点,
∴EF∥PC.
∴∠AEF是异面直线AE与PC所成角或其补角.(7分)
由PA=AB=1,BC=2,计算得AE=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| AE2+EF2-AF2 |
| 2AE•EF |
| ||||||||
2•
|
| ||
| 10 |
∴异面直线AE与PC所成角的余弦值为
| ||
| 10 |
(Ⅲ)解:假设在BC边上存在点G,使得点D到平面PAG的距离为1.
设BG=x,过点D作DM⊥AG于M.
∵PA⊥平面ABCD,
∴PA⊥DM,PA∩AG=A.
∴DM⊥平面PAG.
∴线段DM的长是点D到平面PAG的距离,即DM=1.(12分)
又S△AGD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+x2 |
解得x=
| 3 |
所以,存在点G且当BG=
| 3 |
法二:以A为原点,AB所在直线为x轴,AD所在直线为y轴,
AP所在直线为z轴建立空间直角坐标系,则A(0,0,0),
B(1,0,0),C(1,2,0),
D(0,2,0),E(0,1,),
P(0,0,1).
∴
| CD |
| AD |
| AP |
| AE |
| PC |

(Ⅰ)∵
| CD |
| AD |
∴CD⊥AD.
∵
| CD |
| AP |
∴CD⊥AP.
又AP∩AD=A,
∴CD⊥平面PAD.(5分)
∵CD?平面PAD,
∴平面PDC⊥平面PAD.(7分)
(Ⅱ)∵cos<
| AE |
| PC |
| ||||
|
|
2-
| ||||||
|
| ||
| 10 |
∴异面直线AE与PC所成角的余弦值为
| ||
| 10 |
(Ⅲ)假设BC边上存在一点G满足题设条件,令BG=x,则G(1,x,0).
作DQ⊥AG于Q,
∵PA⊥平面ABCD,
∴PA⊥DQ.
又PA∩AG=A,
∴DQ⊥面PAG.
∴线段DQ的长是点D到平面PAG的距离,即DQ=1.(12分)
∵2S△ADG=S矩形ABCD,
∴|
| AG |
| DQ |
| AB |
| AD |
∴|
| AG |
又AG=
| x2+1 |
∴x=
| 3 |
故存在点G,当BG=
| 3 |
点评:本题考查平面与平面垂直的判定,异面直线所成的角,点到平面的距离,考查逻辑思维能力,空间想象能力,是中档题.

练习册系列答案
相关题目
 已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2.
已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2.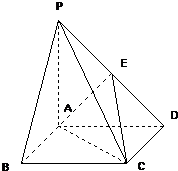 已知:如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=2,E为PD中点.
已知:如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=2,E为PD中点.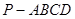 中,四边形
中,四边形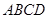 为正方形,
为正方形,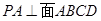 ,且
,且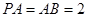 ,
,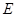 为
为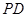 中点.
中点.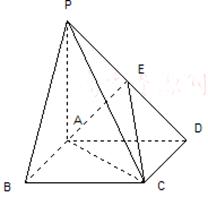
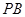 //平面
//平面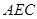 ;
;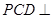 平面
平面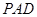 ;
;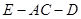 的正弦值.
的正弦值. 中,四边形
中,四边形 为正方形,
为正方形, ,且
,且 ,
, 为
为 中点.
中点. //平面
//平面 ;
; 平面
平面 ;
; 的正弦值.
的正弦值.