题目内容
若函数f（x）=-x2+（2a-1）|x|有四个不同的单调区间，则实数a的取值范围是________．
（
，+∞）
分析：先由函数f（x）=-x2+（2a-1）x变化得到f（x）=-x2+（2a-1）|x|的图象，再将二次函数配方，找到其对称轴，明确单调性，根据图象再研究对称轴的位置即可求解．
解答：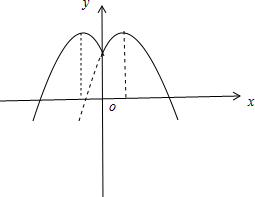
解：f（x）=-x2+（2a-1）|x|可由函数f（x）=-x2+（2a-1）x变化得到：
第一步保留y轴右侧的图象，再作关于y轴对称的图象即可，如图所示：
因为函数有四个不同的单调区间，
所以f（x）=-x2+（2a-1）x的对称轴在y轴的右侧，使y轴右侧有两个单调区间，对称后有四个单调区间．
所以
＞0，即a＞．
故答案为：（，+∞）．
点评：本题考查的知识点是二次函数的性质，其中熟练掌握二次函数的图象和性质是解答本题的关键．
，+∞）分析：先由函数f（x）=-x2+（2a-1）x变化得到f（x）=-x2+（2a-1）|x|的图象，再将二次函数配方，找到其对称轴，明确单调性，根据图象再研究对称轴的位置即可求解．
解答：
解：f（x）=-x2+（2a-1）|x|可由函数f（x）=-x2+（2a-1）x变化得到：第一步保留y轴右侧的图象，再作关于y轴对称的图象即可，如图所示：
因为函数有四个不同的单调区间，
所以f（x）=-x2+（2a-1）x的对称轴在y轴的右侧，使y轴右侧有两个单调区间，对称后有四个单调区间．
所以
＞0，即a＞．故答案为：（
，+∞）．点评：本题考查的知识点是二次函数的性质，其中熟练掌握二次函数的图象和性质是解答本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
若函数f（x）（x∈R）为奇函数，且存在反函数f-1（x）（与f（x）不同），F(x)=
，则下列关于函数F（x）的奇偶性的说法中正确的是（ ）
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F（x）是奇函数非偶函数 |
| B、F（x）是偶函数非奇函数 |
| C、F（x）既是奇函数又是偶函数 |
| D、F（x）既非奇函数又非偶函数 |