题目内容
设集合 ,集合
,集合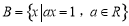 ,则使得
,则使得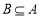 的
的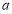 的所有取值构成的集合是( )
的所有取值构成的集合是( )
A.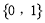 B.
B.
C. D.
D.
练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
题目内容
设集合 ,集合
,集合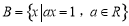 ,则使得
,则使得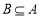 的
的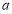 的所有取值构成的集合是( )
的所有取值构成的集合是( )
A.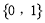 B.
B.
C. D.
D.
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案