题目内容
设z=
|
分析:根据分段函数分段的标准进行分类讨论,分别求出相应区域内的目标函数的最值,从而求出所求.
解答: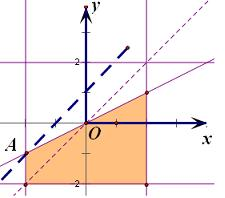 解:当x≥2y时,z=x-y,画出区域图
解:当x≥2y时,z=x-y,画出区域图
平移直线x-y=0,
当过点A(-2,-1)时,直线y=x-z的截距最大,此时z最小
最小值为z=-2-(-1)=-1
当x<2y时,z=y,画出区域图
平移直线y=0,
当过点A(-2,-1)时,直线y=z的截距最小,此时z最小
最小值为z=-1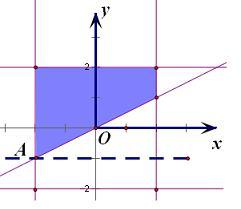
∴z的最小值为-1
故答案为:-1
 解:当x≥2y时,z=x-y,画出区域图
解:当x≥2y时,z=x-y,画出区域图平移直线x-y=0,
当过点A(-2,-1)时,直线y=x-z的截距最大,此时z最小
最小值为z=-2-(-1)=-1
当x<2y时,z=y,画出区域图
平移直线y=0,
当过点A(-2,-1)时,直线y=z的截距最小,此时z最小
最小值为z=-1

∴z的最小值为-1
故答案为:-1
点评:该题的目标函数是一个分段函数,分类讨论是解决本题的关键,本题往往很多同学无从下手,不知所措,将题目分解开来是解题的突破口,是一道易错题.

练习册系列答案
相关题目
设z=
若-2≤x≤2,-2≤y≤2,则z的最小值为( )
|
| A、-4 | B、-2 | C、-1 | D、0 |