题目内容
设z=x+yi(x,y∈R),i是虚数单位,满足4≤z+
≤10.
(1)求证:y=0时满足不等式的复数不存在.
(2)求出复数z对应复平面上的轨迹.
| 64 |
| z |
(1)求证:y=0时满足不等式的复数不存在.
(2)求出复数z对应复平面上的轨迹.
(1)证明:当y=0时,z=x≠0…(2分)
则4≤x+
≤10?
?
…(4分)
由
≥0,因为x2-4x+64>0,则x>0
由
≤0,因为x2-10x+64>0,则x<0
所以不等式无解,满足不等式的复数不存在.…(7分)
(2)4≤x+yi+
≤10,由题知:z+
必为实数…(9分)
所以:
?y=0(舍)或x2+y2=64,2≤x≤5…(12分)
所以z所对应的轨迹是以原点为圆心,以8为半径的圆弧.…(14分)
则4≤x+
| 64 |
| x |
|
|
由
| x2-4x+64 |
| x |
由
| x2-10x+64 |
| x |
所以不等式无解,满足不等式的复数不存在.…(7分)
(2)4≤x+yi+
| 64(x-yi) |
| x2+y2 |
| 64 |
| z |
所以:
|
所以z所对应的轨迹是以原点为圆心,以8为半径的圆弧.…(14分)

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
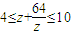 .
.