Question

如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，E为棱BC的中点，F为棱CD上的动点.

(1)试确定点F的位置，使得D₁E⊥平面AB₁F；

(2)当D₁E⊥平面AB₁F时，求二面角B₁AFB的大小.

Answer 1

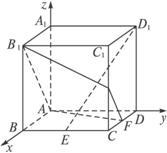
解：(1)如图示，建立空间直角坐标系，则点A(0,0,0)、B₁(1,0,1)、D₁(0,1,1)、E(1,,0)，设F(a,1,0)，=(1,-,-1)，=(a,1,0)，=(1,0,1).

∵D₁E⊥平面AB₁F，∴·=0，·=0，∴a=，即F为棱CD的中点.

(2)平面AB₁F的一个法向量为=(1,-,-1)，平面ABF的一个法向量为=(0,0,1)，

∴cos〈,〉==-.又可知二面角B₁-AF-B为锐二面角，∴二面角B₁-AF-B的大小为arccos.