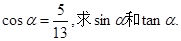题目内容
已知函数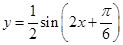 ,
, R.
R.
(1)求它的振幅、周期、初相;
(2)该函数的图象可由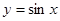 (
( R)的图象经过怎样的平移和伸缩变换得到?
R)的图象经过怎样的平移和伸缩变换得到?
(1)振幅为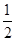 ,周期为
,周期为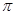 ,初相为
,初相为 ;(2)把函数
;(2)把函数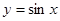 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数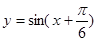 的图象,再把各点的横坐标缩短到原来的
的图象,再把各点的横坐标缩短到原来的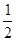 (纵坐标不变)得到函数
(纵坐标不变)得到函数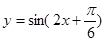 的图象,3、把函数
的图象,3、把函数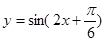 的图象各点的纵坐标缩短到原来的
的图象各点的纵坐标缩短到原来的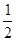 (横坐标不变)得到函数
(横坐标不变)得到函数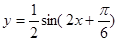 的图象。
的图象。
解析试题分析:(1)函数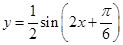 的振幅为
的振幅为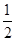 ,周期为
,周期为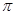 ,初相为
,初相为 .
.
(2)解法1:
1、把函数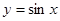 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数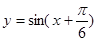 的图象,
的图象,
2、再把各点的横坐标缩短到原来的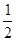 (纵坐标不变)得到函数
(纵坐标不变)得到函数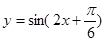 的图象,3、把函数
的图象,3、把函数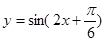 的图象各点的纵坐标缩短到原来的
的图象各点的纵坐标缩短到原来的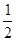 (横坐标不变)得到函数
(横坐标不变)得到函数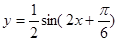 的图象。
的图象。
解法2:
1、函数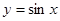 的图象各点的横坐标缩短到原来的
的图象各点的横坐标缩短到原来的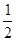 (纵坐标不变)得到函数
(纵坐标不变)得到函数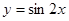 的图象;
的图象;
2、把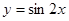 的图象向左平移
的图象向左平移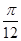 个单位得到函数
个单位得到函数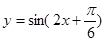 的图象;
的图象;
3、把函数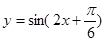 的图象各点的纵坐标缩短到原来的
的图象各点的纵坐标缩短到原来的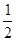 (横坐标不变)得到函数
(横坐标不变)得到函数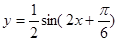 的图象。
的图象。
考点:函数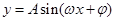 的有关概念;三角函数的图像变换。
的有关概念;三角函数的图像变换。
点评:本题主要考查三角函数图像的变换。对于三角函数图像的变化,我们一定要注意,尤其是其中的平移变换,若x前有系数,一定要先提取系数再加减。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (其中
(其中 >0),且函数
>0),且函数 的最小正周期为
的最小正周期为 .
. 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. ,
, ,函数
,函数 .
. 的最小正周期;(Ⅱ)若
的最小正周期;(Ⅱ)若 ,求函数
,求函数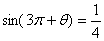 ,
, 的值;
的值;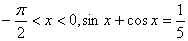 ,求
,求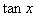 的值。
的值。 .
. 的最小正周期;
的最小正周期; 中,
中, 分别是
分别是 A、
A、 ,
, ,
, ,求
,求 的值.
的值.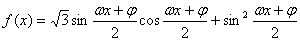
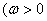 ,
,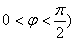 .其图象的最高点与相邻对称中心的距离为
.其图象的最高点与相邻对称中心的距离为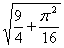 ,且过点
,且过点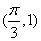 .
. 的达式;
的达式;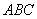 中.
中.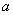 、
、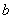 、
、 分别是角
分别是角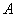 、
、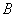 、
、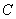 的对边,
的对边,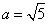 ,
,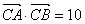 ,角C为锐角。且满足
,角C为锐角。且满足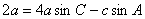 ,求
,求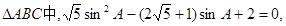 A是锐角,求
A是锐角,求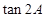 的值;
的值;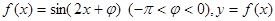 图像的一条对称轴是直线
图像的一条对称轴是直线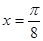 .
.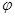 ;(2)画出函数
;(2)画出函数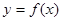 在区间
在区间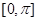 上的图像(在答题纸上完成列表并作图).
上的图像(在答题纸上完成列表并作图).