题目内容
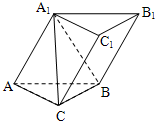 三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,直线A1C与底面成60°角,AB=BC=CA=2,AA1=A1B,则该棱柱的体积为
三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,直线A1C与底面成60°角,AB=BC=CA=2,AA1=A1B,则该棱柱的体积为3
| 3 |
3
.| 3 |
分析:取AB的中点D,连接A1D,CD,由AB=BC=CA=2,AA1=A1B,知A1D⊥AB,CD⊥AB,直线A1C与底面成60°角,所以∠A1CD=60°,CD=
,CA1=2
,A1D=3,A1D是三棱柱ABC-A1B1C1的高,由此能求出该棱柱的体积.
| 3 |
| 3 |
解答:解:取AB的中点D,连接A1D,CD,
∵AB=BC=CA=2,AA1=A1B,
∴A1D⊥AB,CD⊥AB,
∵直线A1C与底面成60°角,
∴∠A1CD=60°,CD=
,CA1=2
,A1D=3,
A1D是三棱柱ABC-A1B1C1的高,
∴S△ABC=
×AB×CD=
.
∴该棱柱的体积V=S△ABC•A1D=3
.
故答案为:3
.
∵AB=BC=CA=2,AA1=A1B,
∴A1D⊥AB,CD⊥AB,
∵直线A1C与底面成60°角,
∴∠A1CD=60°,CD=
| 3 |
| 3 |
A1D是三棱柱ABC-A1B1C1的高,
∴S△ABC=
| 1 |
| 2 |
| 3 |
∴该棱柱的体积V=S△ABC•A1D=3
| 3 |
故答案为:3
| 3 |
点评:本题考查棱柱的体积,是基础题.解题时要认真审题,注意先求出棱柱的底面积和高,再由棱柱的体积公式进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=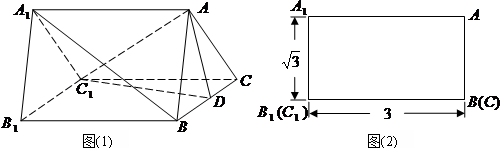
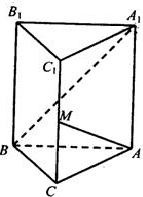 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.