题目内容
一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长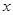 与身高
与身高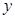 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为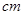 )作为一个样本如上表示.
)作为一个样本如上表示.
|
脚掌长(x) |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
身高(y) |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,做出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程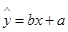 ;
;
(2)若某人的脚掌长为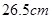 ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率. (参考数据: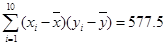 ,
,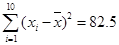 )
)
(1)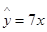 (2)
(2) (3)
(3)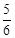
【解析】
试题分析:(1)记样本中10人的“脚掌长”为 ,“身高”为
,“身高”为
 ,
,
则 , 1分
, 1分
∵
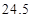 ,
, 3分
3分
∴ 4分
4分
∴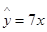 5分
5分
(2)由(20)知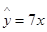 ,当
,当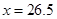 时,
时,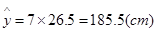 , 6分
, 6分
故估计此人的身高为 。 7分
。 7分
(3)将身高为181、188、197、203(cm)的4人分别记为A、B、C、D, 8分
记“从身高180cm以上4人中随机抽取2人,所抽的2人中至少有1个身高在190cm以上”为事件A,
则基本事件有:(AB)、(AC)、(AD)、(BC)、(BD)、(CD),总数6, 10分
A包含的基本事件有:(AC)、(AD)、(BC)、(BD)、(CD),个数5,
所以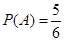 .
12分
.
12分
考点:回归方程与古典概型概率
点评:求回归方程时只需将已知数据代入公式计算即可,在求解时因为数据较多,因此计算要认真,古典概型概率的问题只要是找到所有基本事件种数及满足题意要求的基本事件种数,求其比值即可

一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌长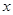 与身高
与身高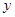 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为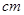 )如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据:
)如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据: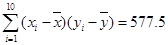 ,
,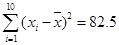 ;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为
;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为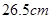 ,则估计案发嫌疑人的身高为
,则估计案发嫌疑人的身高为
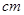 .
.
|
脚长 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
身高 |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |


 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
;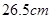 ,试估计此人的身高;
,试估计此人的身高; ,
,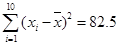 ,
, ,
,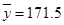 )
)