Question

【题目】若函数的图象上存在两个不同的点、，使得曲线在这两点处的切线重合，称函数具有性质.下列函数中具有性质的有（ ）

A.B.C.D.

Answer 1

【答案】BD

【解析】

根据题意可知性质指函数的图象上有两个不同点的切线是重合的，分析各选项中函数的导函数的单调性与原函数的奇偶性，数形结合可判断A、B选项的正误；利用导数相等，求解方程，可判断C、D选项的正误.综合可得出结论.

由题意可得，性质指函数的图象上有两个不同点的切线是重合的，即两个不同点所对应的导数值相等，且该点处函数的切线方程也相等.

对于A选项，，则，导函数为增函数，不存在不同的两个使得导数值相等，所以A不符合；

对于B选项，函数为偶函数，，

令，可得或，如下图所示：

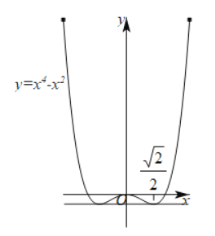
由图象可知，函数在和处的切线重合，所以B选项符合；

对于C选项，设两切点分别为和，则两切点处的导数值相等有：，解得：，令，则，

两切点处的导数，两切点连线的斜率为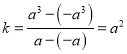，则，得，两切点重合，不符合题意，所以C选项不符合；

对于D选项，，设两切点得横坐标分别为和，

则，所以，

取，，则，，

两切点处的导数值为，两切点连线的直线斜率为，

所以两切点处的导数值等于两切点连线的斜率，符合性质，所以D选项符合.

故选：BD.